Задание По данным об экономических результатах деятельности российских банков(www.finansmag.ru), по данным Банка России (www.cbr.ru/regions), Федеральной службы государственной статистики (www.gks.ru), а также данным изсборников «Национальные счета России» и «Регионы России» (см. www.gks.ru.) выполните следующие задания:
1. Определите параметры уравнения парной линейной регрессии и дайте интерпретацию коэффициента регрессии.
2. Рассчитайте линейный коэффициент корреляции и коэффициент детерминации, поясните смысл этих показателей.
3. С вероятностью 0,95 оцените статистическую значимость каждого параметра и уравнения регрессии в целом.
4. С вероятностью 0,95 постройте доверительный интервал ожидаемого значения результативного признака в предположении, что значение признака фактора увеличится на 5% относительно своего среднего уровня.
Исходные данные для задачи № 1 представлены в книге Excel «МУ.xlsx».
В качестве независимого фактора Х выберем параметр «Средства предприятий и организаций, млн руб», а в качестве зависимого признака Y – «Кредиты предприятиям и организациям, млн руб».
До проведения статистического анализа необходимо установить единую размерность фактора и признака, т.к. средства предприятий указаны в процентах от параметра «Работающие активы». С этой целью значение параметра «Работающие активы» (столбец D листа «Задача 1») умножим на процентную долю фактора «Средства предприятий и организаций» (столбец B листа «Задача 1»). Результат поместим в столбец Е (рис. 1).
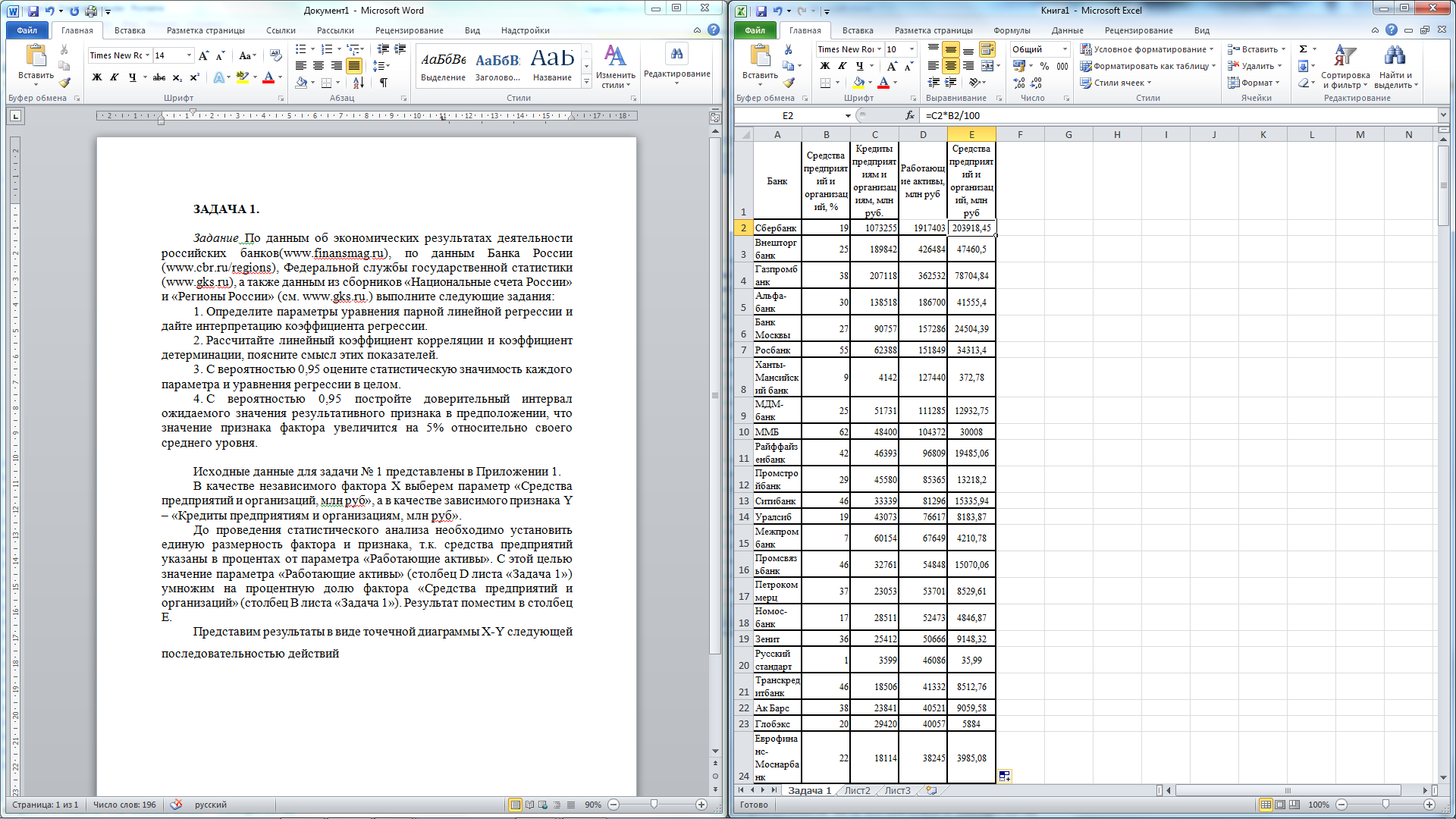
Рис. 1. Предварительная подготовка данных.
В связи с тем, что Excel не очень удобная программа со множеством ограничений, скопируем столбец С в столбец F.
Представим результат в виде точечной диаграммы X-Y следующей последовательностью действий: лента «Вставка», пункт «Диаграммы», «Точечная» (рис. 2).
Затем выбрать пункт «Добавить» и выделить два последних столбца (рис. 3).
В результате получим следующую точечную диаграмму связи фактора с признака (рис. 4).
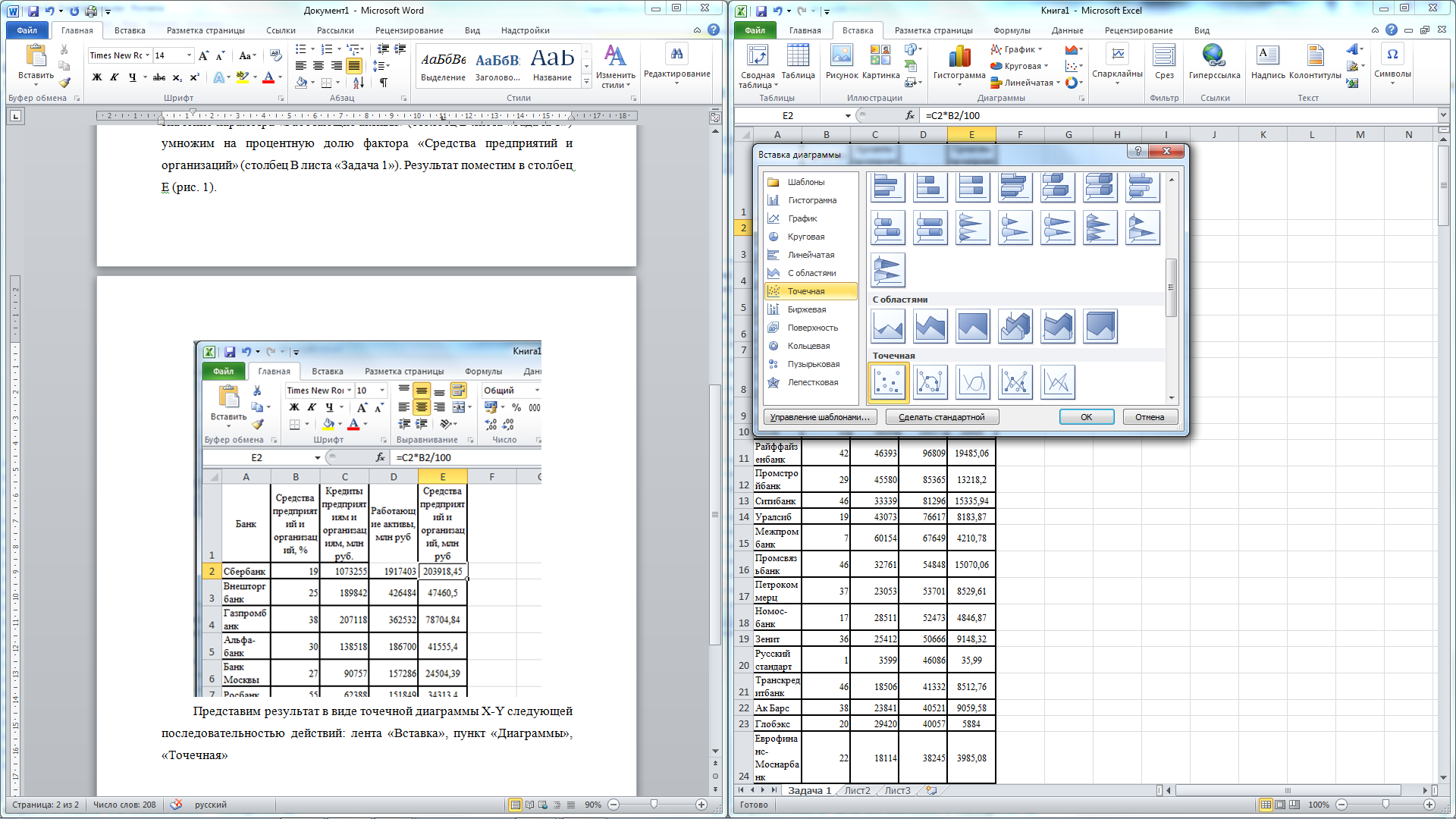
Рис. 2. Вставка рисунка
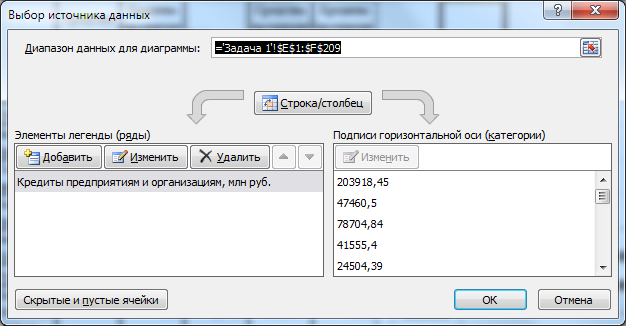
Рис. 3. Выбор данных.
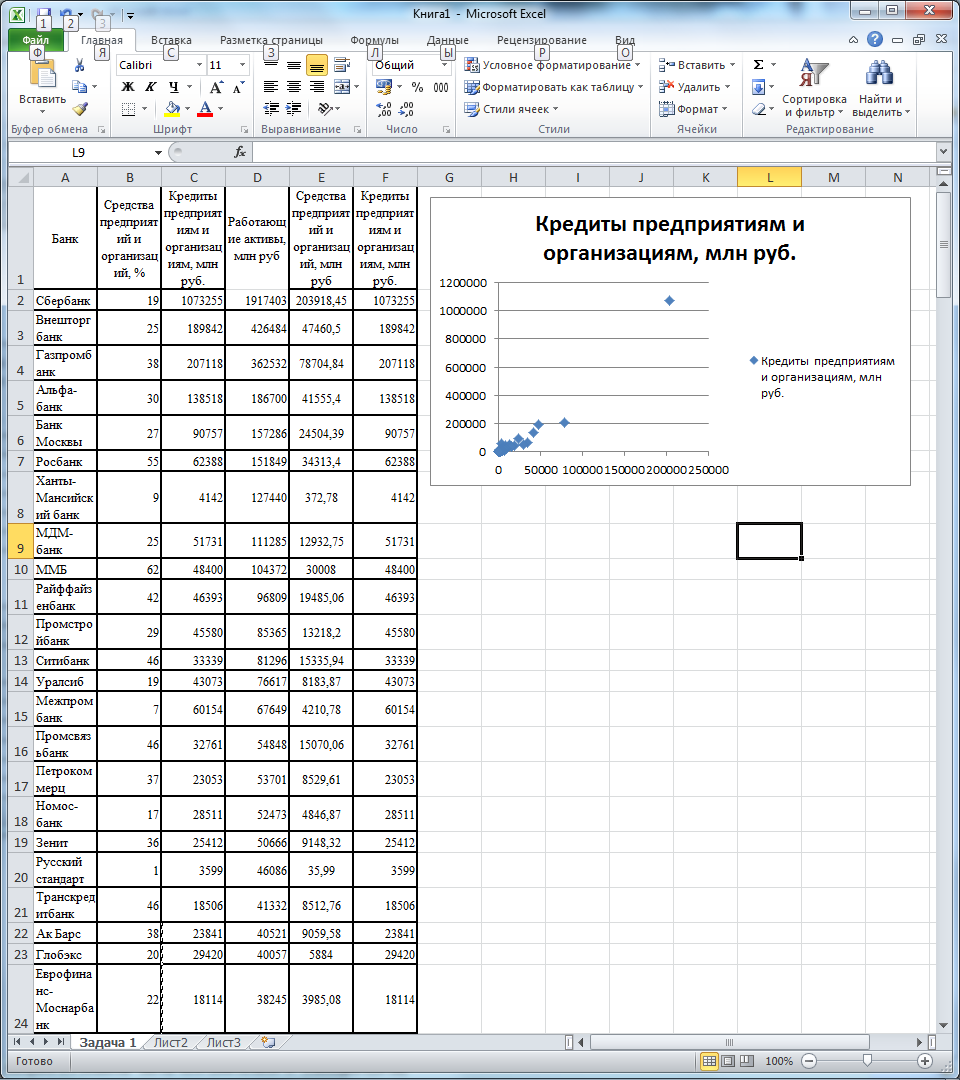
Рис. 4. Предварительный график.
Из рис. 4 можно заметить, что две точки существенно удалены от основной группы. Эти данные необходимо удалить, как неоднородные.
Анализ таблицы показал, что они относятся к Сбербанку (строка 2) и Газпромбанку (строка 4). Скопируем таблицу, перенесем ее на другой лист (Задача 1_1) и удалим эти строки.
Снова построим диаграмму (рис. 5).
Визуальный анализ показывает, что имеются еще две точки, выбивающиеся из основной группы со значением признака Y свыше 100000. Это ВТБ (строка 2), Альфа-банк (строка 3).
Снова перенесем данные на лист «Задача 1_2», удалим эти строки и построим график (рис. 6).
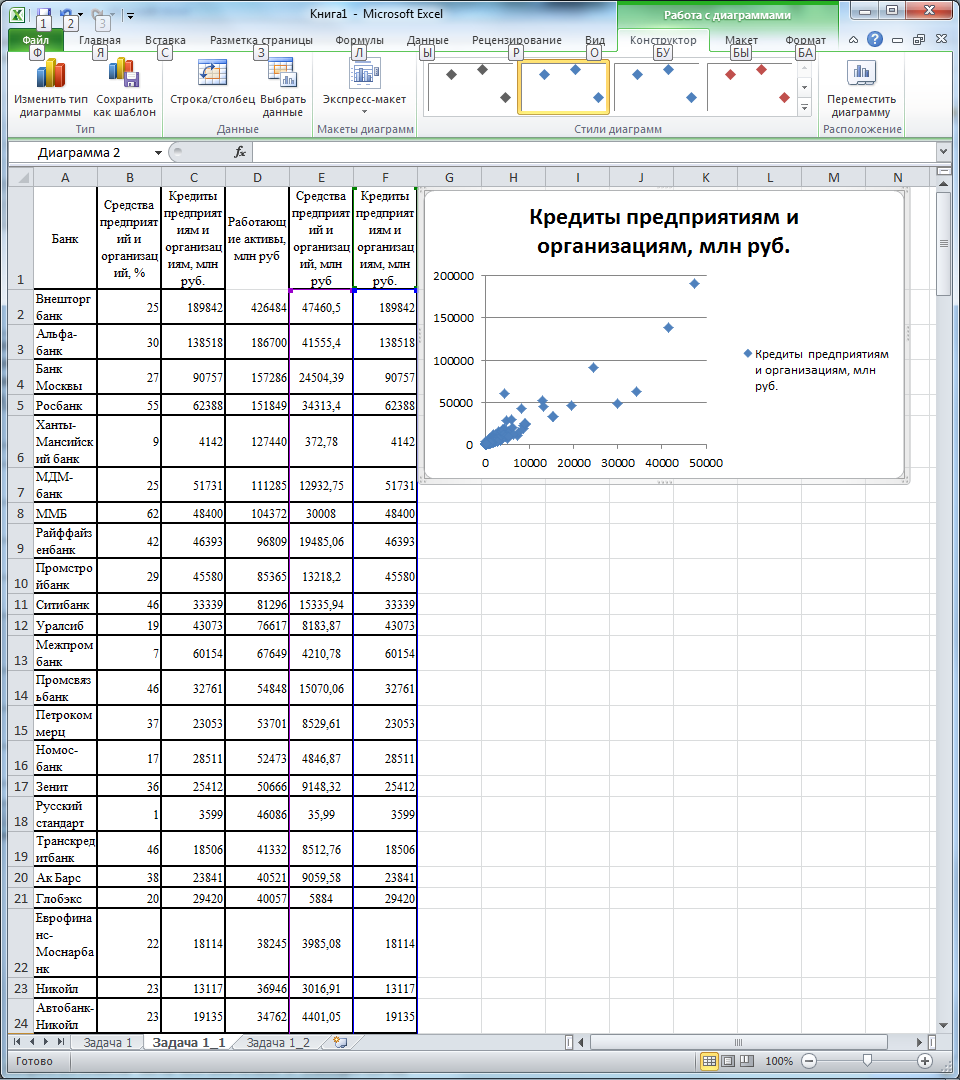
Рис. 5. Второй вариант набора данных
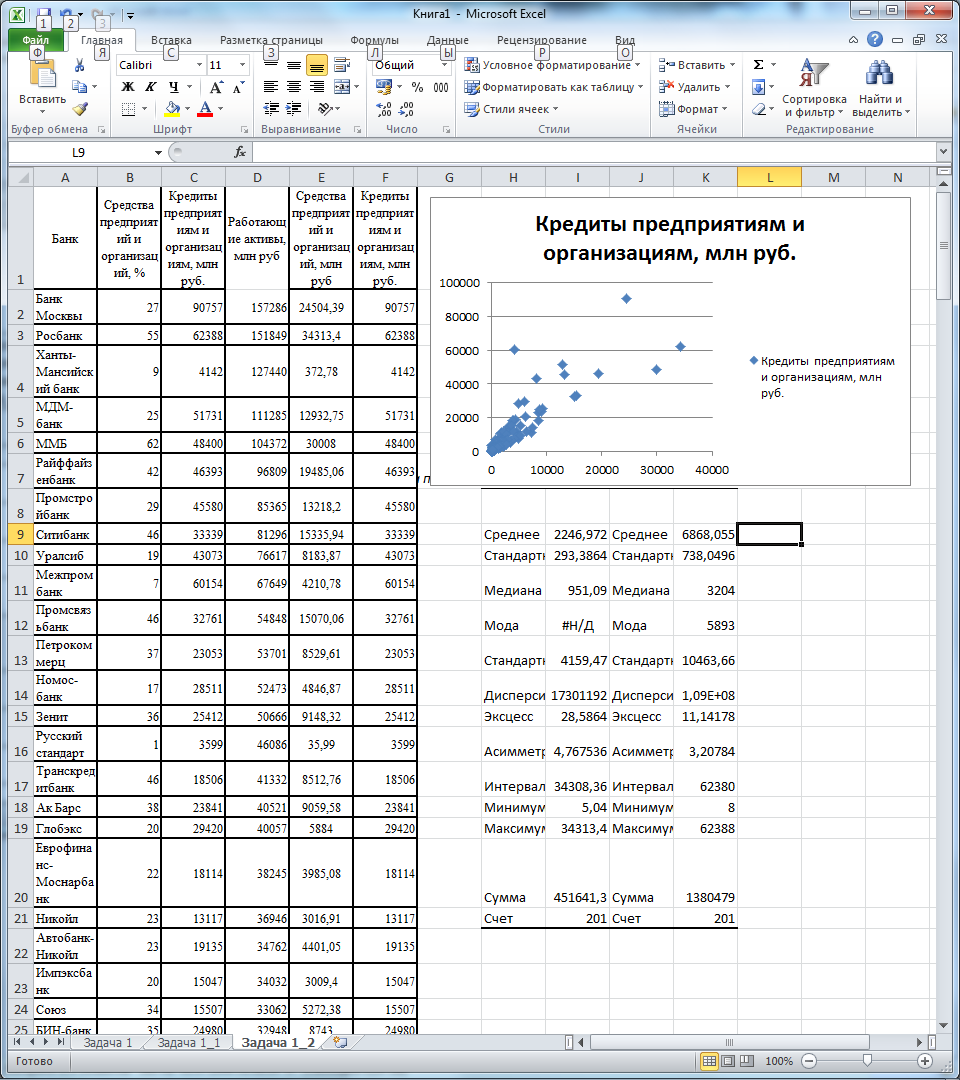
Рис. 6. Третий вариант набора данных
Диаграмма не дает оснований удалить какие-либо данные, поэтому оставляем их без изменений.
Теперь приступаем к выполнению задания.
Строим линейное уравнение регрессии при помощи мастера анализа данных (лента «Данные», пункт «Анализ данных»).
Вначале определяем статистические характеристики переменных:
«Анализ данных» → «Описательная статистика». В панели описательной статистики выбираем входной интервал (столбцы E и F), группирование – «по столбцам», «Метки в первой строке», «Выходной интервал» - любая ячейка в столбце H, «Итоговая статистика» (рис. 7).
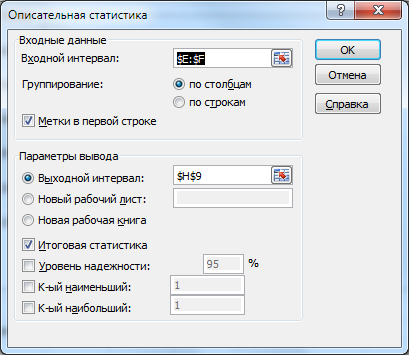
Рис. 7. Заполнение панели «Описательная статистика».
Результаты показаны в табл. 1.
Таблица 1.
Итоговая статистика
| Средства предприятий и организаций, млн руб | Кредиты предприятиям и организациям, млн руб. | ||
| Среднее | 2246,972 | Среднее | 6868,055 |
| Стандартная ошибка | 293,3864 | Стандартная ошибка | 738,0496 |
| Медиана | 951,09 | Медиана | |
| Мода | #Н/Д | Мода | |
| Стандартное отклонение | 4159,47 | Стандартное отклонение | 10463,66 |
| Дисперсия выборки | Дисперсия выборки | 1,09E+08 | |
| Эксцесс | 28,5864 | Эксцесс | 11,14178 |
| Асимметричность | 4,767536 | Асимметричность | 3,20784 |
| Интервал | 34308,36 | Интервал | |
| Минимум | 5,04 | Минимум | |
| Максимум | 34313,4 | Максимум | |
| Сумма | 451641,3 | Сумма | |
| Счет | Счет |
Уравнение регрессии также получаем при помощи мастера «Анализ данных», пункт «Регрессия».
Пример заполнения панели «Регрессия» представлен на рис. 8. При этом не забываем, что признак Y – это столбец Е, а фактор Х – столбец F.
Результаты расчета можно видеть на рис. 9, они приведены в табл. 2…табл.4.
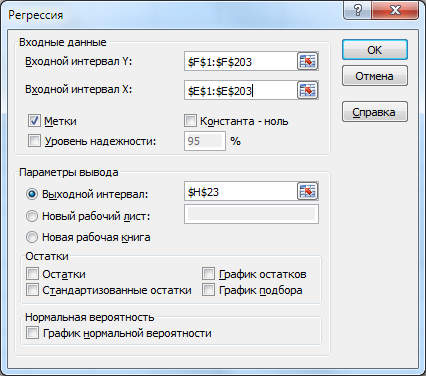
Рис. 8. Заполнение панели «Регрессия».
Таблица 2.
| Регрессионная статистика | |
| Множественный R | 0,874631 |
| R-квадрат | 0,764979 |
| Нормированный R-квадрат | 0,763804 |
| Стандартная ошибка | 5827,586 |
| Наблюдения |
Таблица 3.
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 2,21E+10 | 2,21E+10 | 650,9865 | 8,3E-65 | |
| Остаток | 6,79E+09 | ||||
| Итого | 2,89E+10 |
Таблица 4.
| Коэффици-енты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | a=1709,052 | 464,6013 | 3,678534 | 0,000302 | 792,906 | 2625,197 |
| Средства предприятий и организаций, млн руб | b=2,364838 | 0,092686 | 25,51444 | 8,3E-65 | 2,182071 | 2,547606 |
В табл. 2 указано, что множественный коэффициент корреляции R=0,875. Таким образом изменение признака Y на 87,5% объясняется изменением признака X. Дисперсионный анализ (табл.3) показывает, что значимость критерия Фишера составляет 8,3∙10-65, что существенно ниже, чем 1-α=1-0,95=0,05. Это говорит о тесной линейной связи и адекватности уравнения регрессии.
По табл. 4 можно написать уравнение регрессии:
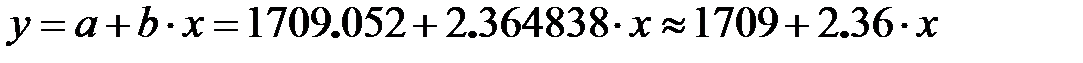
p -значение коэффициентов уравнения регрессии во много раз меньше 5%, следовательно все они значимы.
Построим теперь прогноз признака Y при значении фактора Х, равном 105% от его среднего значения.
По данным табл. 1 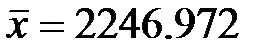 , следовательно 105% от него равны
, следовательно 105% от него равны 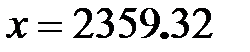
По уравнению регрессии найдем значение Y:
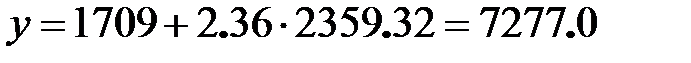
Ошибку прогноза найдем по формуле
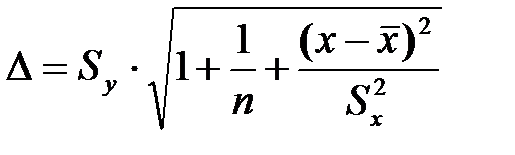
Здесь Sy – среднее квадратическое отклонение признака Y; Sx – среднее квадратическое отклонение фактора Х; n – объем выборки; х – значение признака, для которого необходимо вычислить прогноз; 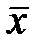 - среднее значение фактора Х.
- среднее значение фактора Х.
Все эти значения представлены в табл. 1:
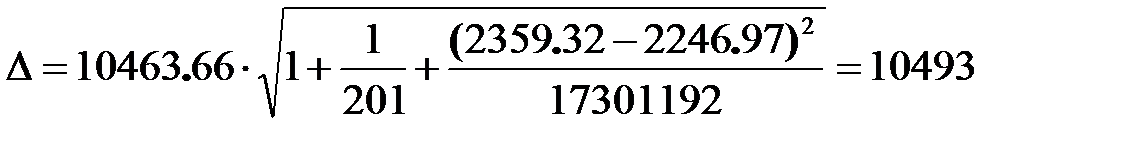
Большую величину ошибки можно объяснить очень большими эксцессами и асимметриями. Подавляющее большинство точек сгруппированы около начала координат.
 2015-05-18
2015-05-18 1709
1709