Следствие. Все -мерные векторные пространства имеют одну и ту же арифметическую модель, поэтому изоморфны

Все 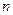-мерные векторные пространства имеют одну и ту же арифметическую модель, поэтому изоморфны.

Множество многочленов степени не выше 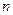в примере 1 образуют 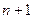-мерное пространство. Изоморфизм, устанавливающий размерность, задается в этом случае так

, .

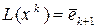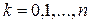Здесь 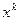– мономы, а 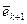– базисные орты в .

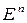Если векторное пространство 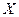содержит для всякого 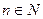подмножество, 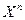, которое само является векторным пространством и для него выполняется аксиома размерности с заданным 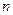, то 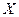назовем бесконечным векторным пространством. Примером такого пространства является множество всех многочленов. Подмножества многочленов степени не выше 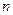образуют 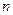-мерные подпространства в этом пространстве.