Проведя полное исследование множественной зависимости Кредитов от Средств предприятия и Выпущенных ценных бумаг, можно сделать вывод:
1) интеркоррелированность между факторами Средств предприятия и Выпущенных ценных бумаг не существует.
2) информативный набор факторов состоит из одного признака. Им может быть любой из вышеупомянутых факторов:
3) коэффициент детерминации R2= 0,0599 (скорректированный R2 = 0,0038);
4) ранжирование частных корреляций не выявляет цепочку предпочтений: факторы x3 и x4 равноправны.
5) В таблице 8.1 представлен сравнительный анализ моделей регрессии.
Средние показатели эластичности факторов:
Таблица 8.1 – Сравнительный анализ результатов регрессий 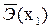
| F | 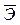
| Параметры | А | |
| Линейная форма с полным набором факторов | надежно: R2 =0,9077 | 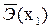 = -0,2357% = -0,2357%
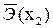 =0.1285% =0.1285%
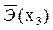 =0,792% =0,792%
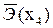 = -0,057% = -0,057%
| значимым признается лишь параметр х3 | 10,35% |
| Линейная форма с информативными факторами х1, х2, х3 | надежно: R2 = 0,9064 | 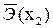 =0.165% =0.165%
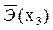 =0,7075% =0,7075%
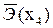 = -0,057% = -0,057%
| значимым признается лишь параметр х3 | 10,3% |
| Линейная форма с информативными факторами х3, х4 | надежно: R2 = 0,9023 | 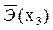 =0,826% =0,826%
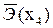 =–0,045% =–0,045%
| значимым признается лишь параметр х3 | 10,37% |
| Мультипликативная форма с полным набором факторов | надежно | 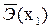 = 3,0065% = 3,0065%
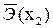 =0,5595% =0,5595%
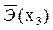 =0,267% =0,267%
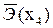 = –0,715% = –0,715%
| Все параметры являются незначимыми | 12,2% |
| Мульт. форма с факторами х1, х2, х3 | 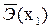 = 4,0833% = 4,0833%
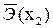 =0,3939% =0,3939%
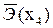 = –0,3965% = –0,3965%
| Все параметры являются значимыми | 12,35% | |
| Мульт. форма с факторами х1, х2 | 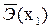 = 3,2454% = 3,2454%
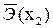 =0,1158% =0,1158%
| Все параметры являются незначимыми | 13,2% | |
| Мульт. форма с фактором х1, | 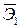 = 4,2325 = 4,2325
| Все параметры значимыми | 13,53% |
Проанализировав 7 моделей регрессии, можно сделать вывод, что применимой для описания зависимости между эксплуатационной длиной магистральных трубопроводов и эксплуатационными длинами остальных видов путей сообщения, тыс. км является линейная модель с полным набором факторов или с факторами х1, х2, х3
Однако если рассматривать модели с точки зрения каждого полученного показателя, то самыми высокими коэффициентами эластичности и всеми значимыми параметрами обладает линейная форма с информативными факторами. Самая низкая ошибка аппроксимации у линейной формы с полным набором факторов.
5) Все предпосылки метода наименьших квадратов выполняются, за исключением четвертой предпосылки (об отсутствии автокорреляции в остатках).
9) Выполним расчет прогнозного значения результата, предполагая, что прогнозные значения факторов составят 104,2% от их среднего уровня.
Имеем: 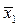 , = 31,9,
, = 31,9, 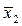 = 11,79
= 11,79
Новые значения переменных:
х1 = 1,042 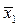 = 1,042·31,9 = 33,24; х2 = 1,042
= 1,042·31,9 = 33,24; х2 = 1,042 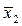 = 1,042·11,79 = 12,285
= 1,042·11,79 = 12,285
у = 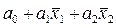 =
=
= 30032,4–308,094·33,24–454,15·12,285 = 30032,4–10241,0–5579,2 = 14212,1
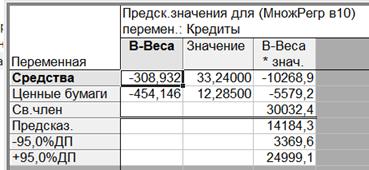
Таким образом, получим доверительный интервал для прогнозного значения у при х1 = 33,24; х2 = 12,285:
3369,6 < ŷ < 24999,1
 2015-05-18
2015-05-18 371
371








