2015-05-18
1528
Пусть задано дифференциальное уравнение и начальные условия, определяющие частное решение. Допустим, что решение уравнения в окрестности точки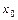 
, в которой заданы начальные условия, можно разложить в степенной ряд, по степеням разности 
:
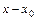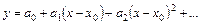
Продифференцируем этот ряд с неопределенными пока коэффициентами столько раз, каков порядок уравнения. Подставляя затем в уравнение вместо неизвестной функции и ее производных соответствующие ряды, получаем тождество, из которого определяем неизвестные коэффициенты ряда. При этом первые коэффициенты ряда (в числе, равном порядку уравнения) определяются не из тождества, а из начальных условий. Если далее доказать, что полученный ряд сходится, то можно быть уверенным, что он выражает искомое решение.
Особенно удобно с помощью рядов решать линейные дифференциальные уравнения.
Пример 18. Найти решение уравнения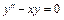 
при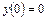 
, 
.
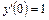Решение.
Решение будем искать в виде ряда, разложенного по степеням 
:
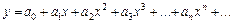
Коэффициенты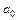 
и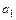 
находим из начальных условий:
, 
.
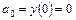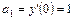Дважды дифференцируем ряд:
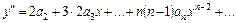
Подставляя в дифференциальное уравнение вместо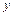 
и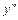 
их разложения, получаем тождество
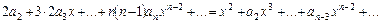
Сравнивая коэффициенты при одинаковых степенях , находим:
, 
,…, 
.
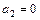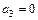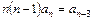Поэтому
, 
, 
, 
, 
, 
, 
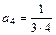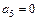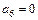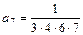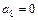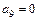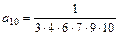
и вообще
, 
.
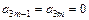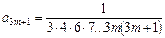Значит,
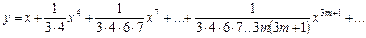
С помощью признака Даламбера легко убедиться, что этот ряд сходится на всей оси 
и, следовательно, представляет искомое решение при всех .
