Ряд Тейлора

Определение. Рядом Тейлора функции 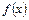в окрестности точки 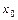называется степенной ряд

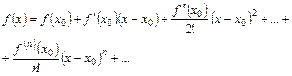(34)

относительно разности 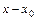, коэффициенты которого 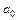, ,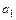…, ,… 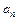выражаются через функцию 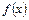и ее производные в точке 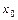по формулам

, , ,…, ,…

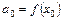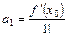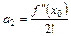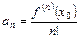Эти коэффициенты называются коэффициентами Тейлора функции 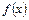в точке .

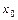Обозначим через 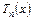многочлен 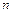-ой степени, равный сумме первых 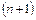членов ряда Тейлора:

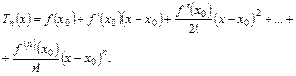
Разность

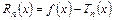
называется остаточным членом ряда Тейлора.

Для того, чтобы ряд Тейлора при значении сходился и имел своей суммой 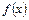, т.е.

,

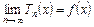необходимо и достаточно, чтобы

,

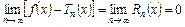т.е. остаточный член ряда Тейлора должен стремиться к нулю при .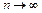

Заметим, что особенно часто используется разложение функций по степеням . В этом случае, полагая в (34) 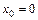, получаем ряд

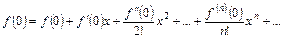, (35)

который называется рядом Маклорена.