Определение. Коэффициентами Фурье функции 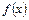 называются числа
называются числа 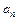 и
и 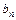 , определяемые формулами
, определяемые формулами
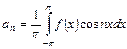 ,
, 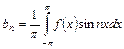 . (36)
. (36)
Ряд
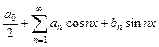 (37)
(37)
называется рядом Фурье функции 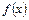 .
.
В случае разложения в ряд Фурье функции, заданной в интервале 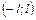 , где
, где 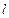 - произвольное число, формулы (36) и (37) принимают вид:
- произвольное число, формулы (36) и (37) принимают вид:
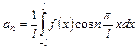 ,
, 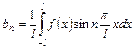 . (38)
. (38)
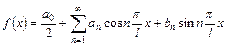 . (39)
. (39)
Пример 19. Разложить в ряд Фурье функцию 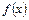 на отрезке
на отрезке 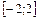 .
.
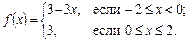
Решение.
По формулам (38) найдем:
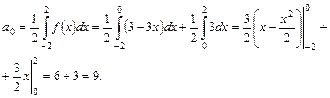
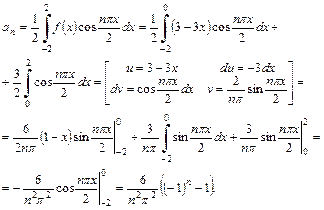
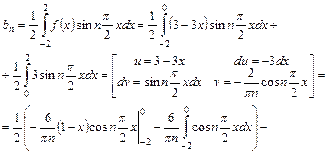
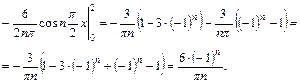
Подставим найденные значения коэффициентов ряда Фурье в формулу (38):
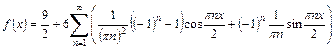 .
.
_________________________________________
Решение 0-варианта
(часть2)
1. Вычислить неопределенные интегралы:
а) 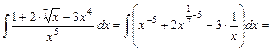
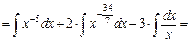
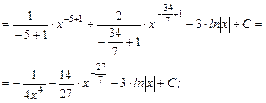
б) 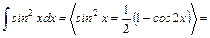
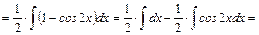
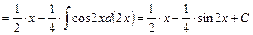 ;
;
в) 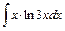 . Используем формулу интегрирования по частям:
. Используем формулу интегрирования по частям: 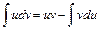 , где
, где 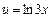 ,
, 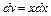 ;
; 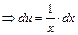 ,
, 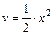 . Т.о.:
. Т.о.:
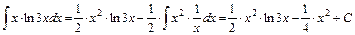 ;
;
г) 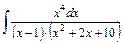 . Перемножаем скобки в знаменателе и делим числитель на знаменатель:
. Перемножаем скобки в знаменателе и делим числитель на знаменатель:





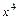
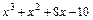
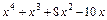
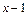
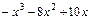
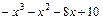

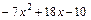
Найдем дискриминант 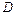 выражения
выражения 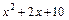 :
: 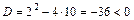 . Т.о., уравнение
. Т.о., уравнение 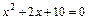 не имеет вещественных корней и интеграл запишется в виде:
не имеет вещественных корней и интеграл запишется в виде:
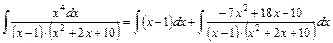 .
.
Первый интеграл решается легко. Во втором интеграле (обозначим его 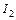 ) по формуле (7) проводим разложение подынтегральной функции на простые дроби:
) по формуле (7) проводим разложение подынтегральной функции на простые дроби:
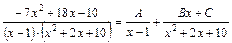 .
.
Приводим к общему знаменателю правую часть равенства и приравниваем числители в обеих частях равенства:
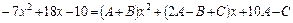 .
.
Приравниваем коэффициенты при одинаковых степенях  слева и справа:
слева и справа:
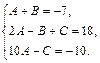
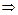
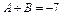 ,
, 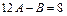
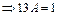
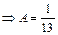 ,
, 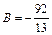 ,
, 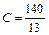 .
.
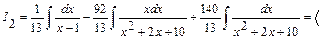 в числителе 2 – го интеграла формируем дифференциал знаменателя:
в числителе 2 – го интеграла формируем дифференциал знаменателя: 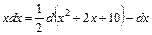
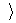
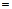
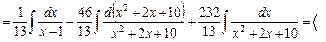 знаменатель последнего интеграла приводим к полному квадрату:
знаменатель последнего интеграла приводим к полному квадрату: 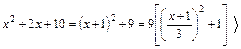 . Т.о., последний интеграл выражается через арктангенс. Окончательно получим:
. Т.о., последний интеграл выражается через арктангенс. Окончательно получим:
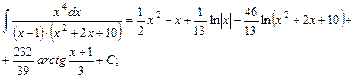
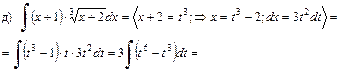
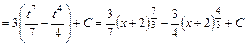 .
.
 2015-05-18
2015-05-18 594
594








