1. Показательная функция 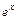 разлагается в ряд Маклорена при всех значениях
разлагается в ряд Маклорена при всех значениях  , т.е. при
, т.е. при 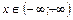 :
:
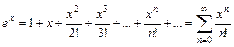 .
.
2. Тригонометрические функции 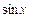 и
и 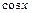 разлагаются в ряд Маклорена при всех значениях
разлагаются в ряд Маклорена при всех значениях  , т.е. при
, т.е. при 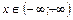 :
:
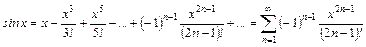 .
.
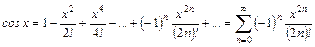 .
.
3. Биномиальный ряд представляет функцию 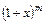 в интервале
в интервале 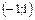 :
:
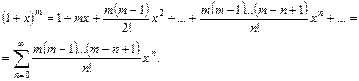
Заметим, что данная формула справедлива в случае, когда m не является натуральным числом (в противном случае ряд обрывается).
4. Логарифмическая функция 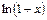 разлагается в ряд Маклорена в интервале
разлагается в ряд Маклорена в интервале 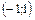 :
:
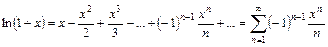
5. Арктангенс 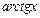 разлагается в ряд Маклорена в интервале
разлагается в ряд Маклорена в интервале 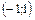 :
:
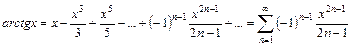 .
.
Пример 17. Разложим в ряд Маклорена функцию 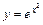 .
.
Решение. Заменим в формуле
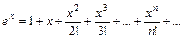
 на
на 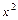 . Получим:
. Получим:
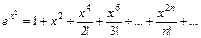
Ответ: 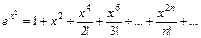
 2015-05-18
2015-05-18 454
454








