Доказательство методом исключения строится на конструкции исключения, к которой затем применяется метод противоречия. Если нужно доказать теорему 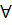 x
x 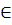 M: A(x)
M: A(x) 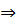 В(х) методом исключения, то наряду с заключением В(х) рассматривают все остальные возможности:
В(х) методом исключения, то наряду с заключением В(х) рассматривают все остальные возможности: 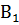 (х),
(х),  (х), …,
(х), …, 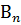 (х). Затем предполагают, что вместо заключения В(х) имеет место
(х). Затем предполагают, что вместо заключения В(х) имеет место 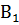 (х), и показывают, что это приводит к противоречию. Так поступают и со всеми остальными возможностями:
(х), и показывают, что это приводит к противоречию. Так поступают и со всеми остальными возможностями:  (х), …,
(х), …, 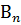 (х). В результате остается лишь одна возможность:
(х). В результате остается лишь одна возможность: 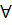 x
x 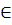 M: A(x)
M: A(x) 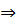 В(х).
В(х).
Обычно такой метод доказательства применяется там, где нужно использовать аксиому трихотомии (для любых чисел а и b возможно одно из трех: а = b, а < b, а > b).
Рассмотрим теорему: «В треугольнике квадрат стороны, лежащей против острого угла, меньше суммы квадратов двух других сторон». Доказательство этой теоремы можно провести методом исключения. Вначале предположим, что квадрат этой стороны равен сумме квадратов двух других сторон, и получим противоречие; затем предположим, что квадрат этой стороны больше суммы квадратов двух других сторон, и опять получим противоречие; эти два противоречия позволяют заключить, что возможно только одно: квадрат стороны, лежащей против острого угла треугольника, меньше суммы квадратов двух других сторон.
Проиллюстрируем доказательство методом исключения на такой теореме:
«Для того чтобы две прямые в пространстве были параллельны, необходимо и достаточно, чтобы всякая плоскость, пересекающая одну из них, пересекала бы и другую».
Докажем и необходимость указанного условия, и его достаточность. При доказательстве достаточности как раз и будет использован метод исключения.
Доказательство
I. Условие необходимо. Пусть а 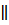 b, причем а и b принадлежат плоскости
b, причем а и b принадлежат плоскости 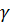 . Плоскость
. Плоскость 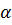 , пересекающая прямую а, пересечет и плоскость
, пересекающая прямую а, пересечет и плоскость 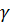 . Пусть плоскости
. Пусть плоскости 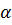 и
и 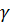 пересекаются по прямой l. Прямая l, пересекая одну из параллельных прямых — а, должна пересечь и другую прямую — b. Точка пересечения прямых l и b как раз и будет единственной общей точкой плоскости
пересекаются по прямой l. Прямая l, пересекая одну из параллельных прямых — а, должна пересечь и другую прямую — b. Точка пересечения прямых l и b как раз и будет единственной общей точкой плоскости 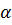 и прямой b.
и прямой b.
II. Условие достаточно. Пусть любая плоскость, пересекающая прямую а, пересекает и прямую b. Прямые а и b не могут быть пересекающимися, так как тогда существует плоскость, пересекающая а и не пересекающая b. Прямые а и b не могут быть и скрещивающимися, так как тогда существует плоскость, пересекающая прямую а и не пересекающая прямую b. По методу исключения остается только одно: прямая а параллельна прямой b.
Примером метода исключения может служить доказательство теоремы Ферма из курса алгебры и начал анализа: «Если функция f(x) на интервале (а; b) достигает своего наибольшего или наименьшего значения в точке 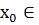 (а; b) и в этой точке она дифференцируема, то f'’(
(а; b) и в этой точке она дифференцируема, то f'’(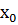 ) = 0».
) = 0».
Введем обозначения: через 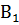 (х) обозначим факт f'’(
(х) обозначим факт f'’(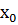 ) = 0, через
) = 0, через  (х) обозначим факт f'’(
(х) обозначим факт f'’(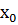 )
) 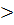 0, через
0, через  (х) обозначим факт f'’(
(х) обозначим факт f'’(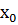 ) < 0. Очевидно, что никакие два из предложений
) < 0. Очевидно, что никакие два из предложений 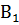 (х),
(х),  (х),
(х),  (х) не могут быть одновременно истинными, но одно из них обязательно истинно. Для доказательства теоремы достаточно показать, что ложно
(х) не могут быть одновременно истинными, но одно из них обязательно истинно. Для доказательства теоремы достаточно показать, что ложно  (х) и ложно
(х) и ложно  (х), тем самым будет утверждена истинность
(х), тем самым будет утверждена истинность 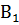 (х).
(х).
 2015-05-20
2015-05-20 1438
1438
