Свободные электромагнитные колебания

Свободными (собственными) электромагнитными ко­лебаниями называют такие, которые совершаются без внешнего воздействия за счет первона­чально накопленной энергии.

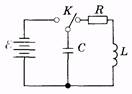Рассмотрим колебательный контур, состоящий из резистора R, катушки индуктивности L и конденсатора С (рис. 14.1); сопротивлением проводов и возможным излучением электромагнитных волн пренебрегаем. Конденсатор ключом К заряжается от источника *, а затем разряжается на резистор и катушку индуктивности. При этом в контуре возникает ЭДС

самоиндукции 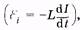, которая, согласно закону Ома, будет Рис. 14.1 равна сумме напряжений на элементах цепи: на резисторе U_R = IR и конденсаторе 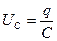. Поэтому запишем

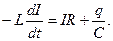(14.1)

Преобразуем это уравнение, поделив все члены на L и учитывая, что 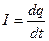и :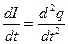

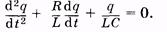(14.2)

Это есть дифференциальное уравнение свободных электроманитных колебаний. Произведя замены:

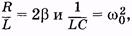(14.3)

получим уравнение

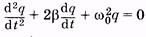(14.4)

Незатухающие колебания. Если контур не содержит резистора (рис. 14.2), то из (14.4) имеем:

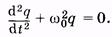(14.5)

Известно, что (14.5) является дифференциальным уравнением гармонического колебания, его решение [см. (5.8)] имеет вид

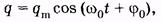(14.6)

где q _m— наибольший (начальный) заряд на обкладках конденсатора, w₀ — круговая частота собственных колебаний (собственная круговая частота) контура, j₀ — начальная фаза.

По гармоническому закону изменяется не только заряд на обкладках конденсатора, но и напряжение, и сила тока в контуре, соответственно:

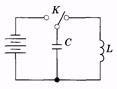Рис. 14.2 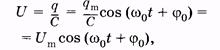(14.7)

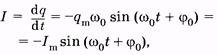(14.8)

где U _m и I _т — амплитуды напряжения и силы тока.

Графики зависимости заряда (напряжения) от времени аналогичны графику зависимости смещения x(t), а график зависимости силы тока от времени — графику скорости u (t) (см. рис. 5.4).

Из (14.3) найдем выражение для периода собственных колебаний (формула Томсона):

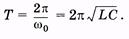(14.9)

Затухающие колебания. При наличии резистора (рис. 14.1) процесс в контуре описывается уравнением (14.4), которое аналогично уравнению (5.19) для механических колебаний. При условии, что затухание не слишком велико, то есть 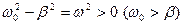находим следующее решение [см. (5.20)]:

(14.10)

График этой функции аналогичен графику на рис. 5.6. Если затухание мало (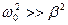), то w» w₀. В этом случае логарифмический декремент затухания

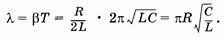(14.11)

Апериодический разряд конденсатора на резистор (силь­ное затухание). При сильном затухании 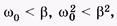или, используя (14.3),

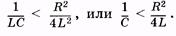(14.12)

Неравенство (14.12) выполняется, в частности, в контуре при отсутствии индуктивности (L ® 0). Для этого случая (разряд кон­денсатора на резистор) из (14.1) имеем

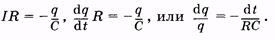(14.13)

Интегрируя последнее уравнение, находим

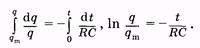(14.14)

Потенцируя второе из выражений (14.14), имеем

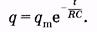(14.15)

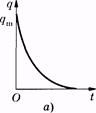
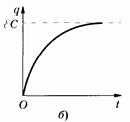
Рис. 14.3

Уравнение (14.15) описывает процесс разрядки конденсатора С на резистор R. При отсутствии индуктивности колебания не воз­никают (рис. 14.3, а). По такому закону изменяется и напряжение на обкладках конденсатора. Теоретически такой процесс, как это следует из (14.15), протекает бесконечно долго, однако принято длительность подобных процессов оценивать временем, в течение которого параметр, характеризующий процесс (в данном случае заряд и напряжение), уменьшится в е раз (постоянная времени, t).

Выражение для постоянной времени можно получить из (14.15), если вместо q подставить 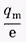, a t заменить на t: 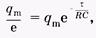откуда для контура с конденсатором и резистором постоянная времени равна

t = RС. (14.16)

Можно показать, что зарядка конденсатора от источника постоянной ЭДС * также происходит по экспоненциальному закону

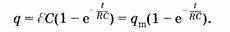(14.17)

График этой зависимости представлен на рис. 14.3,6.