Не всегда удобно рассматривать систему в виде сложной САУ
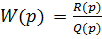
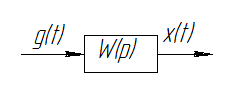
Поэтому выделяют отдельные элементы, которые можно свести к общим.
Основные типы звеньев делятся на 3 группы:
· Позиционные
· Дифференцирующие
· Интегрирующие
► Позиционные:
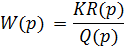
Описываются следующие оператором, где R(p), Q(p) – имеют свободные члены.
В стандартной форме коэффициент равен единице.
► Дифференцирующие:
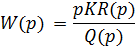
R(p), Q(p) – свободные члены
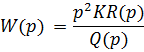
Двукратнодифференцировано.
► Интегрирующие:
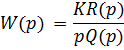
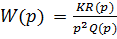
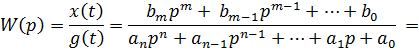
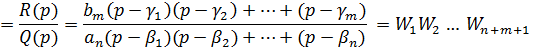
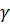 – корни числителя
– корни числителя
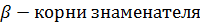
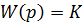 - безынерционное звено.
- безынерционное звено.
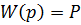 ;
; 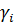 = 0 - звено чистого дифференцирования
= 0 - звено чистого дифференцирования
Дифференцирующее звено 1 порядка
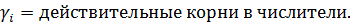
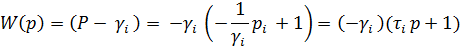
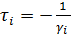 - постоянная времени
- постоянная времени
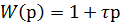 .
.
Идеальное интегрирующее звено
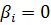
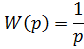
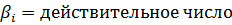
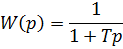
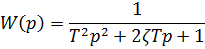
T – постоянная времени
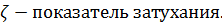
Если 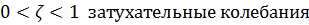
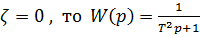 - консервативное звено.
- консервативное звено.
Дифференцирующее звено 2 порядка
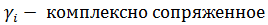

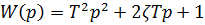
Описываются линейными ДУ.
Удобно решать с использованием преобразования Лапласа.
f(t) → F(S) S- комплексная переменная
f(t) – оригинал, F(S) – изображение.
Решать ДУ проще, заменяя операции на простые.
Исследование САУ происходит во временной и частотной области.
Временная область: работает с переменными x(t)
Частотная область: x(S)
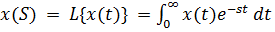 - линейный оператор
- линейный оператор
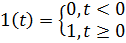
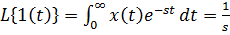 – преобразования Лапласа
– преобразования Лапласа
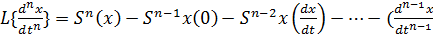 )
)
Пример:
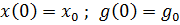
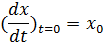
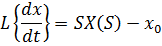
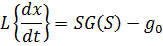
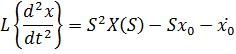
Если
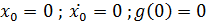
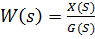
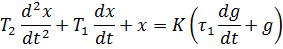
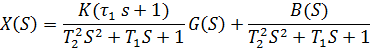
B(S) – многочлен с величинами начальных условий
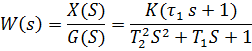
Передаточная функция W(s) - это отношение изображения входного сигнала по Лапласу к выходному сигналу изображения при нулевых начальных условиях.
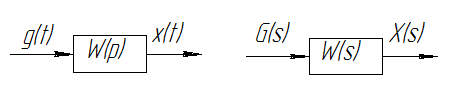
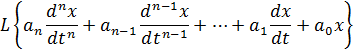
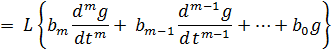
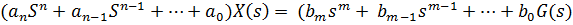
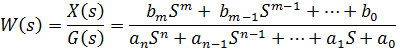
При нулевых начальных условиях.
Виды передаточных функций:
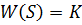
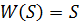
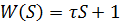
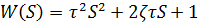
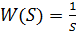
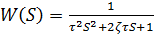
 2015-05-12
2015-05-12 1051
1051








