Корневой годограф (КГ) – совокупность траекторий, перемещение корней характеристического уравнения замкнутой системы при изменении какого-нибудь параметра системы.
Например.
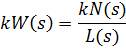
Передаточная функция разомкнутой системы.
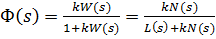
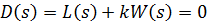
Другая форма записи:
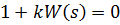
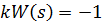 - основное уравнение метода КГ.
- основное уравнение метода КГ.
Пусть корни характеристического уравнения S1, S2, …. Sn замкнутой системы. Далее, полюса передаточной функции разомкнутой системы L(s)
P1, p2 …. Pn
Передаточная функция разомкнутой системы:
N(s) N1, N2, …. Nm (m<n) m –знаменатель n – числитель.
Pi Nj - не зависят от коэффициентов усиления разомкнутой системы.
Задача. Расположение Pi Nj на комплексной плоскости корней (для разомкнутой системы).
kW(s)
Найти характеристические корни Si замкнутой системы как функцию параметра К (к.у. разомкнутой системы) т.е. построить корневой годограф.
Корни характеристического уравнения являются полюсами передаточной функции замкнутой системы.
Нули передат. функции замкнутой системы совпадают с нужными передаточными функциями разомкнутой системы.
Основное уравнение корневого годографа можно разделить на уравнение модулей и уравнение фаз:
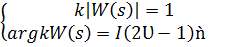
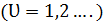
Представим уравнение разомкнутой системы в виде произведения корней и полюсов.
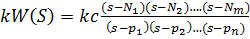 (n>m)
(n>m)
C N(s) L(s)
С – отношение коэффициента при старших членах от многочленов N(s) и L(s).
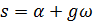
На комплексной плоскости будет вектор.
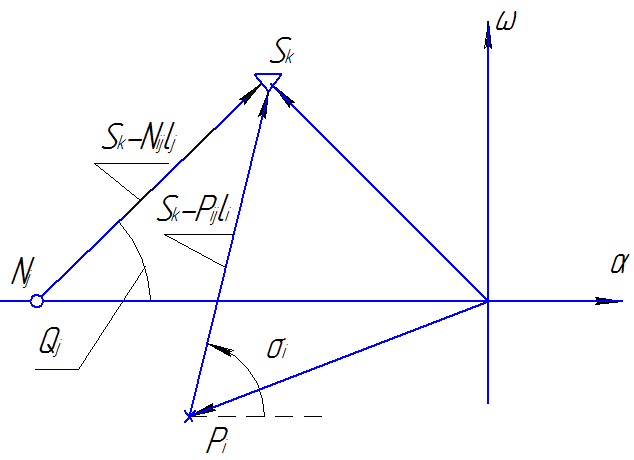
Рис 17.1
Х – полюса
0 – Нули
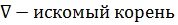
Пол.
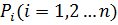
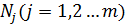
kW(s)
каждый из векторов имеет модуль и аргумент.
Sk – Nj 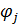
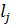
Фаза модуль
Sk – Ni 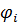
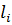
Тогда уравнение фаз:
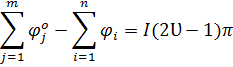
Уравнение фаз не зависит от параметра k.
Уравнение модуля: 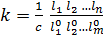
Решение задачи.
Найти положение sk, которое удовлетворяет уравнению фаз при любых значениях pi и Nj.
Уравнение модулей (посчитать величину k0 уравнению модулей).
Постепенно построить весь корневой годограф.
Пример.
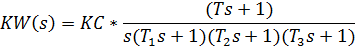
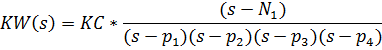
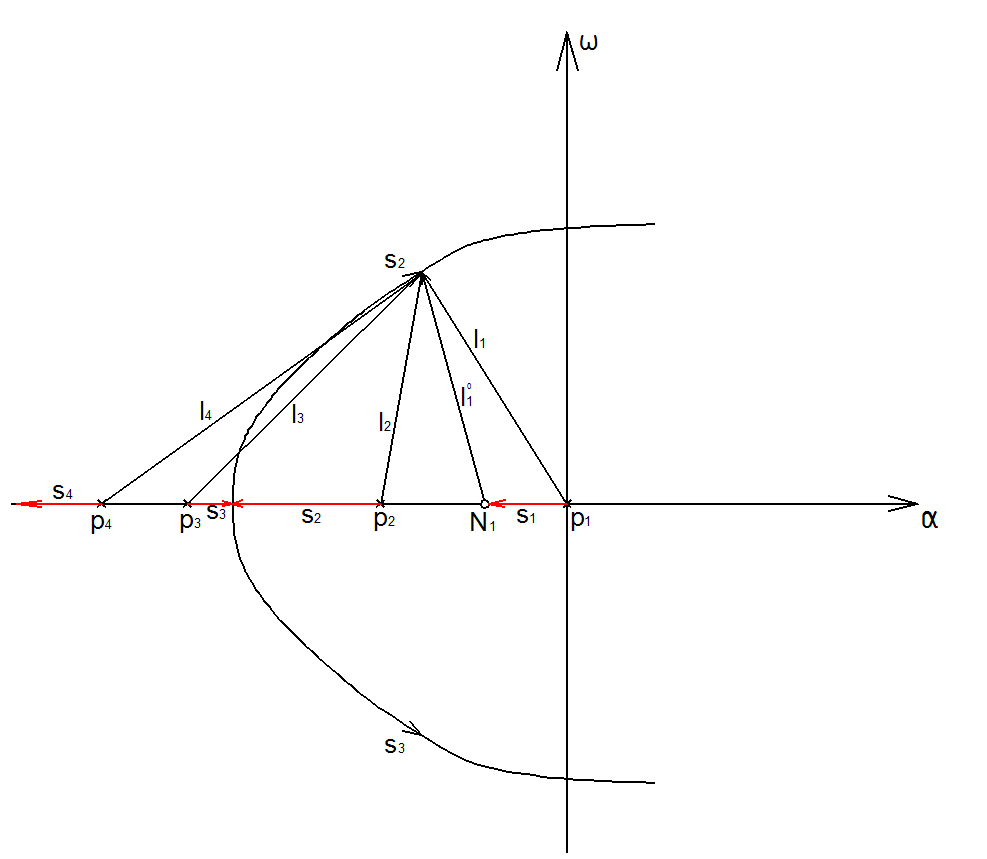
Рис 17.2
Где
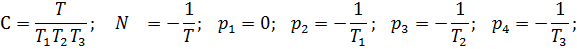
si – корни характеристического уравнения замкнутой системы.
При K=0 sk совпадает с pi.
Уравнение фаз: 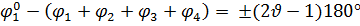
Уравнение фаз для s1 будет выполняться, если он находится между точками p1 и N1.
Для s4: действительная ось и левее p4 .
При увеличении К точки движутся по стрелочкам.
Для s2 и s3: уравнение фаз выполняется, если они находятся между p2 и p3. При увеличении К – движутся навстречу, могут слиться. При дальнейшем увеличении К пойдут по дугам (станут комплексными).
Из уравнения модулей:
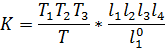
 2015-05-12
2015-05-12 2684
2684







