Краткие теоретические сведения. Пусть функция имеет производную в каждой точке интервала

Пусть функция имеет производную в каждой точке интервала 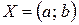. Обозначим 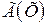дугу графика функции , соответствующую интервалу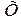

Если дуга 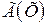лежит не ниже (не выше) касательно к графику функции , проведенной в любой точке 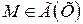, то функцию называют выпуклой вниз (выпуклой вверх) в интервале .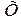

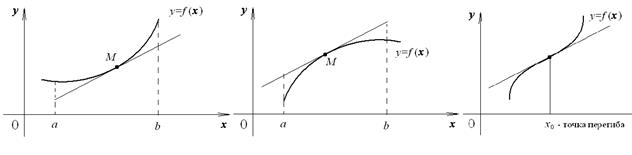
Точку на графике функции называют точкой перегиба функции или графика функции, если она является границей дуг графика с разными направлениями выпуклости.

Теорема 1. Если функция имеет вторую производную в интервале 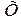и в каждой точке 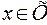выполняется 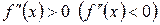, то является выпуклой вниз (выпуклой вверх) в интервале Х.

Теорема 2. Если точка 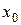является точкой перегиба функции , то либо 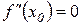, либо 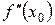не существует.

Теорема 3. Если слева и справа от точки 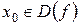вторая производная 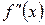существует и имеет родные знаки, то в точке 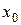график функции имеет перегиб.

Алгоритм исследования функции

Шаг 1. Найти область определения функции .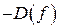

Шаг 2. Проверить наличие у исследуемой функции дополнительных свойств (четность, нечетность, периодичность).

Шаг 3. Найти точки пересечения графика с осями координат

Шаг 4. Найти 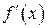и интервалы монотонности и экстремумы функции.

Шаг 5. Найти 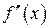и интервалы выпуклости и точки перегиба функции….

Шаг 6. Построить эскиз графика .