2015-05-10
540
Задание 1. Найти интервалы выпуклости и точки перегиба графика функции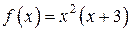 
.
Решение:
Шаг 1.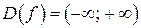 
.
Шаг 2. Найти вторую производную функции 
.
,
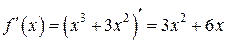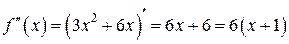
Шаг 3. Найдем точки, в которых по Теореме 2 может оказаться перегиб графика функции:
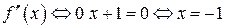
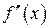существует во всех точках 
.
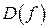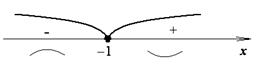
Шаг 4. Разбить 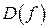точками возможного перегиба на части и определить знак 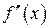в каждом из полученных интервалов.
|
.
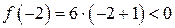
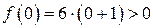Шаг 5. Определить промежутки выпуклости и точки перегиба графика функции
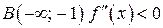, следовательно, по Теореме 1 выпукла вверх.
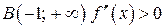, следовательно, по Теореме 1 выпукла вниз.
По Теореме 3 в точке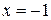 
график имеет перегиб.
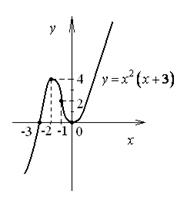
Задание 2. Исследовать функцию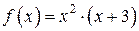 
.
Решение:
Шаг 1. .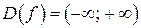
Шаг 2.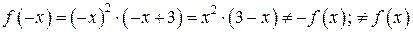 
.
Функция не является ни четной, ни нечетной, ни периодической
Шаг 3. Точки пересечения с осями
О х: 
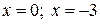
| О у: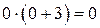 
|
| Точки (0; 0), (-3; 0) | Точки (0; 0) |
Шаг 4.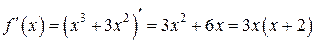 
|
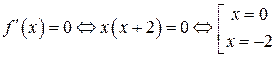
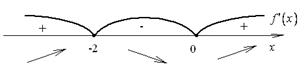
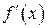всюду существует в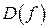
Функция возрастает в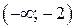 
и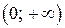 
, убывает в (-2; 0).
Точка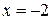 
есть точка максимума. Точка 
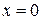есть точка минимума функции.
|
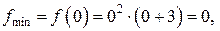
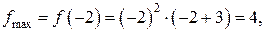
Шаг 5. Как определили в задание 1, выпукла вниз в 
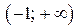, выпукла вверх в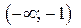 
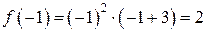
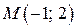- точка перегиба графика
Шаг 6.
