Определение. Будем говорить, что распределение вероятностей непрерывной случайной величины является равномерным распределением, если плотность вероятности случайной величины Х имеет вид:
f(x)= 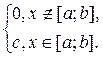
Найдем значение с.
Так как плотность вероятности удовлетворяет условию:
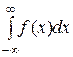 =1,
=1,
то получаем:
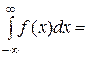
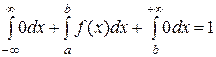 .
.
Так как f(x)=c на промежутке [a;b], то 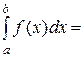
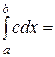
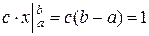 , следовательно, c =
, следовательно, c = 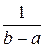 .
.
Итак, равномерно распределённая случайная величина имеет плотность вероятности:
f(x)= 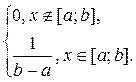
Пример. Если распределение случайной величины Х – равномерное и задан отрезок [2;8], то b – a = 8 – 2 = 6 и
f(x)= 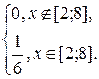
Найдем числовые характеристики равномерного распределения.
1. Математическое ожидание равномерного распределения.
М(Х)=  =
= 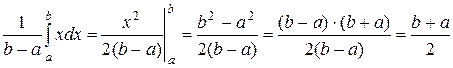 .
.
 2015-05-12
2015-05-12 1783
1783
