Аналитические и статистические методы

Кратко охарактеризуем особенности, достоинства и недостатки этих классов методов с точки зрения возможности использования при моделировании (представлении) систем.

Аналитическими в рассматриваемой классификации названы методы, которые отображают реальные объекты и процессы в виде точек, совершающих какие-либо перемещения в пространстве или взаимодействующих между собой в соответствии с определенными соотношениями, имеющими силу закона.

Основу понятийного (терминологического) аппарата этих представлений составляют понятия классической математики: величина, формула, функция, уравнение, система уравнений, логарифм, дифференциал, интеграл и т. д. Для аналитических представлений характерно не только стремление к строгости терминологии, но и к закреплению за некоторыми специальными величинами определенных букв (символов). Например, удвоенное отношение площади круга к площади вписанного в него квадрата - 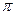, основание натурального логарифма - , …

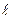На базе аналитических представлений возникли и развиваются математические теории различной сложности – от аппарата классического математического анализа до таких сравнительно новых разделов современной математики, как математическое программирование (линейное, нелинейное, динамическое и т. п., теория игр (матричные игры с чистыми стратегиями, дифференциальные игры и т. п.).

Эти теоретические направления стали основой многих прикладных, в том числе, таких как теория автоматического управления, теория оптимальных решений и т. д.

При моделировании систем применяется широкий спектр символических представлений, использующих «язык» классической математики. Однако далеко не всегда эти символические представления адекватно отражают реальные сложные процессы. Большинство из направлений математики не содержит средств постановки задачи и доказательства адекватности модели. Последняя доказывается экспериментом, который по мере усложнения проблем также становится все более сложным, дорогостоящим, не всегда бесспорен и реализуем.

В то же время в состав этого класса методов, как было указано, входит такое относительно новое направление математики, как математическое программирование, которое содержит средства постановки задачи и расширяет возможности доказательства адекватности модели. Привлекательность методов математического программирования для решения слабоформализованных задач (каковыми, как правило, являются задачи планирования, распределения работ и ресурсов, загрузки оборудования и другие задачи управления современным предприятием на начальном этапе их постановки) объясняется рядом особенностей, отличающих эти методы от методов классической математики:

- вводятся понятия целевая функция и ограничения, которые являются фактически некоторыми средствами постановки задачи;

- дается представление об области допустимых решений;

- появляется возможность объединения в единой модели разнородных критериев (измеряемых в разных единицах – метрах, килограммах, штуках и т. п.), что очень важно при отображении реальных проектных и производственных ситуаций;

- модель математического программирования допускает (и даже ориентирует на это) выход за границу области определения переменных, в то время как методы классической математики требуют введения строгих начальных и граничных условий, значений которых не может принимать переменная в процессе анализа модели;

- изучение методов решения задач математического программирования позволяет получить представление о пошаговом приближении к решению, т. е. пошаговом алгоритме получения результатов моделирования.

Обратим внимание на то, что аналитические методы применяются в тех случаях, когда свойства системы можно отобразить с помощью детерминированных величин и зависимостей, т. е. когда знания о процессах и событиях в некотором интервале времени позволяют полностью определить поведение их вне этого интервала.

Эти методы используются при решении задач движения и устойчивости, оптимального размещения, распределения работ и ресурсов, выбора наилучшего пути, оптимальной стратегии поведения, в том числе в конфликтных ситуациях, и т. п.

В то же время при практическом применении аналитических представлений для отображения сложных систем следует иметь в виду, что они требуют установления всех детерминированных связей между учитываемыми компонентами и целями системы в виде аналитических зависимостей. Для сложных многокомпонентных, многокритериальных систем и задач получить требуемые аналитические зависимости крайне трудно. Более того, даже если это и удается, то практически невозможно доказать правомерность применения таких выражений, т. е. адекватность модели рассматриваемой задаче.

В этих ситуациях следует обращаться к другим методам моделирования.

Статистические представления сформировались как самостоятельное научное направление в середине XIX века (хотя возникли значительно раньше). Основу их составляет отображение процессов и явлений с помощью случайных (стохастических) событий, поведение которых описывается соответствующими вероятностями (статистическими характеристиками и статистическими закономерностями).

Статистические отображения системы в общем случае (по аналогии с аналитическими) можно представить в виде как бы «размытой» точки (размытой области) в n-мерном пространстве, в которую переводит систему (или ее учитываемые в модели свойства) некоторый оператор. При этом «размытую» точку следует понимать как некоторую область, характеризующую движение системы (ее поведение); при этом границы области заданы с некоторой вероятностью 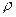(«размыты») и движение точки описывается некоторой случайной функцией.

Закрепляя все параметры этой области, кроме одного, можно исследовать зависимость поведения системы от значений этого параметра – получить статистическое распределение по параметру (одномерное). Аналогично можно получить двумерную, трехмерную и т. д. картины статистического распределения. В формализованном виде эти зависимости представляются в виде соответствующих законов распределения случайных величин и их числовых характеристик.

Практическое применение получили, в основном, одномерные распределения, что связано со сложностью получения статистических закономерностей и доказательства их адекватности для конкретных приложений, которые базируются на понятии выборки и ее количественных характеристик.

На базе статистических представлений развивается ряд математических теорий, которые изучают отдельно: математическая статистика (объединяющая различные методы статистического анализа); теория статистических испытаний (основой которой является метод Монте-Карло); развитие этой теории – теория статистического имитационного моделирования; теория выдвижения и проверки статистических гипотез, базирующаяся на общей теории статистических решающих функций Вальда; теория потенциальной помехоустойчивости; обобщающая последние два направления теория статистических решений, в рамках которой, в свою очередь, возникли новые полезные для практики направления.

Перечисленные направления в большинстве своем носят теоретико-прикладной характер и возникали из потребностей практики. В то же время есть ряд дисциплин, которые носят более выраженный прикладной характер. В их числе: статистическая радиотехника, статистическая теория распознавания образов, экономическая статистика, теория массового обслуживания, а также развившиеся из направлений, возникших на базе аналитических представлений, стохастическое программирование, новые разделы теории игр и т. п.

Расширение возможностей отображения сложных систем и процессов по сравнению с аналитическими методами можно объяснить тем, что при применении статистических представлений процесс постановки задачи как бы частично заменяется статистическими исследованиями, позволяющими, не выявляя все статистические связи между изучаемыми объектами (событиями) или учитываемыми компонентами сложной системы, на основе выборочного исследования (исследования представительной (репрезентативной) выборки) получать статистические закономерности и распространять их на поведение системы в целом.

Однако, если не удается доказать репрезентативность выборки или для этого требуется недопустимо большое время, то применение статистических методов может привести к неверным результатам.

В таких случаях целесообразно обратиться к методам, объединяемым под общим названием – методы дискретной математики, которые помогают разработать языки моделирования, модели и методики постепенной формализации процесса принятия решения.