Параметри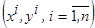ческие алгоритмы восстановления стохастических зависимостей

Пусть дана статистически независимых наблюдений случайной величины 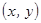, распределённых с неизвестной плотностью 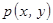. Также имеется информация о виде искомой зависимости (3.1), представленная в полиномиальном виде 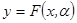. Необходимо построить параметрическую оценку регрессии 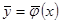, если известно, что оператор связи 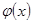имеет однозначный характер.

Для простоты последующих выкладок предположим, что зависимость описывается полиномом

.

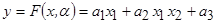Задача восстановления стохастической зависимости (3.1) сводится к определению неизвестных коэффициентов полинома (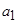, , 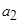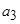) из условия минимума квадратического критерия (3.2) с помощью метода наименьших квадратов.

Необходимо подобрать коэффициенты полинома таким образом, чтобы сумма квадратов отклонений полинома от экспериментальных точек была минимальна

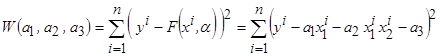. (3.2)

Для этого необходимо приравнять к нулю производные критерия (3.2) по 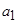, 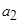и :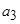

,

,

.

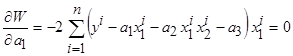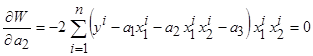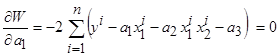После очевидных преобразований, полученную систему уравнений можно представить в матричном виде

.

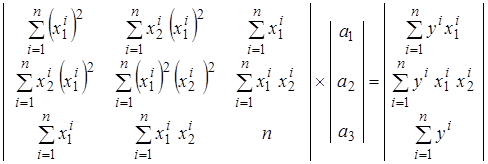Воспользовавшись методом Гаусса приводим матрицу к треугольному виду и находим неизвестные коэффициенты полинома.

В итоге получаем параметрическую оценку регрессии

,

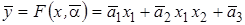где 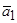, , 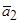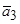- рассчитанные коэффициенты.