2015-05-13
1431
Пусть дана выборка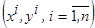 
статистически независимых наблюдений случайной величины 
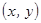, распределённых с неизвестной плотностью 
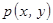. Априори вид искомой стохастической зависимости (3.1) не задан. Необходимо построить непараметрическую оценку регрессии 
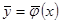, если известно, что оператор связи 
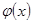имеет однозначный характер.
Для того, чтобы построить хорошую модель по своим точностным характеристикам выберем среднеквадратический критерий
,
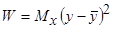который характеризует меру близости модели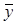 
к точкам обучающей выборки.
Найдём минимум критерия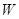 
, приравняв к нуль производную
.
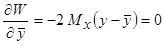В итоге получаем
.
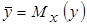Оптимальное решающее правило в смысле минимума среднеквадратического критерия представляется в виде условного математического ожидания
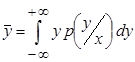, (3.3)
где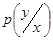 
- условная плотность вероятности, которую можно записать в виде отношения
.
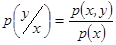Подставим в вместо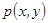 
и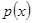 
их оценки плотности вероятности типа Розенблатта-Парзена (2.2), получим
,
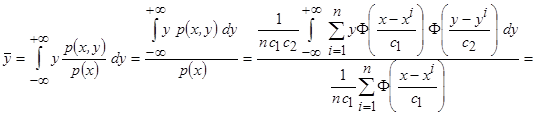
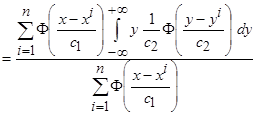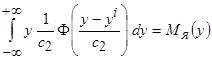- математическое ожидание случайной величины 
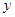с ядерной плотностью 
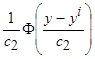(ядерная функция положительная, симметричная и площадь под ней равна единицы).
|
|
|
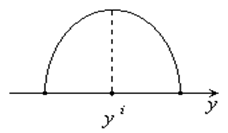Рис. 3.3. Ядерная функция
|
Учитывая, что ядерная функция является симметричной, получаем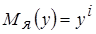
 ,
т.к. ядерная функция строится вокруг точки  .
|
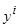Тогда непараметрическая оценка регрессии принимает вид
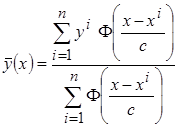. (3.4)
Если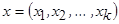 
- многомерная случайная величина, то непараметрическая оценка регрессии запишется в виде
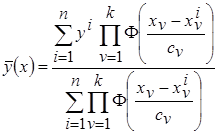. (3.5)
Для трёхмерной случайной величины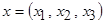 
непараметрическая оценка регрессии принимает вид:
.
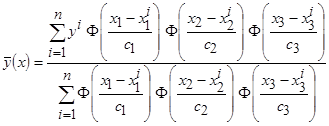С позиций принципов коллективного оценивания непараметрическая оценка регрессии является частным случаем коллектива
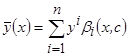, (3.6)
где
.
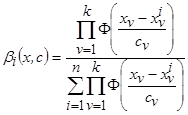В рассматриваемой оценке наблюдения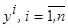 
восстанавливаемой функции играют роль элементов коллектива, а многомерные ядерные функции представляются в виде их весов.
