Для упрощения доказательства, предположим, что закон распределения аргументов 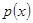 известен. Тогда непараметрическая оценка регрессии принимает (3.4) вид
известен. Тогда непараметрическая оценка регрессии принимает (3.4) вид
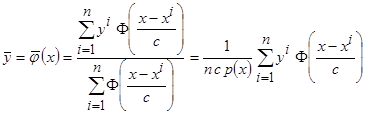 . (3.7)
. (3.7)
1. Асимптотическая несмещённость 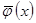 , при которой
, при которой
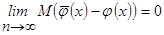 .
.
Методика доказательства асимптотических свойств аналогична теореме 3.1.
Для проверки свойства несмещённости покажем, что
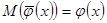 .
.
Подставим вместо 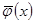 оценку (3.7)
оценку (3.7)
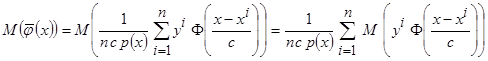 .
.
Представим математическое ожидание в интегральной форме
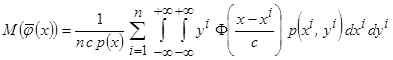 .
.
Так как 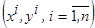 наблюдения одной и той же случайной величины
наблюдения одной и той же случайной величины 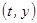 , то
, то 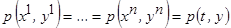 .
.
Тогда
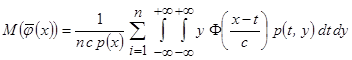 .
.
Распишем совместную плотность вероятности 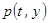 в виде произведения
в виде произведения 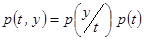 .
.
В результате получим
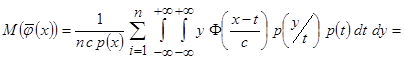
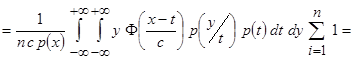
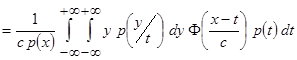 .
.
Учитывая, что 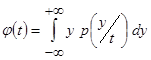 - условное математическое ожидание (3.3) и проведя замену переменных
- условное математическое ожидание (3.3) и проведя замену переменных 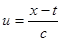 ,
, 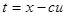 ,
, 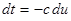 и т.д., получаем
и т.д., получаем
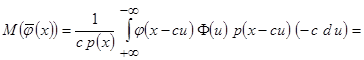
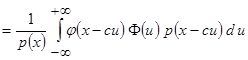 .
.
Разложим функции 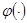 и
и 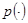 в ряд Тейлора в точке
в ряд Тейлора в точке 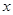 .
.
Тогда
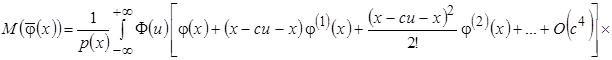
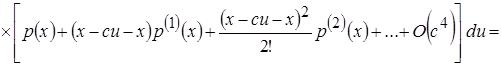
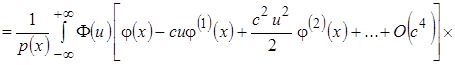
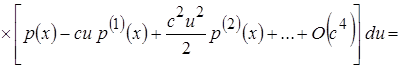
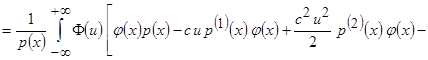
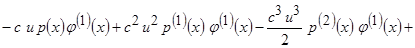
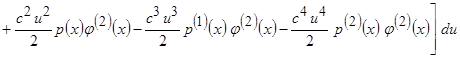 .
.
Учитывая, 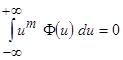 при нечётном значении
при нечётном значении 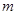 и
и 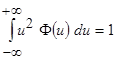 (см. теорему 3.1).
(см. теорему 3.1).
После сокращений получаем выражение соответствующее асимптотической несмещённости
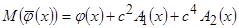 , (3.8)
, (3.8)
где
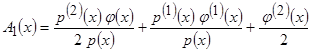 ,
,
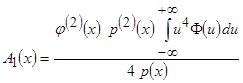 .
.
Отсюда следует, что непараметрическая оценка регрессии в асимптотике (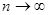 ) стремится к оптимальному решающему правилу (условному математическому ожиданию) при
) стремится к оптимальному решающему правилу (условному математическому ожиданию) при 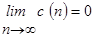 .
.
2. Сходимость в среднеквадратическом
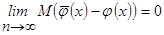 .
.
 2015-05-13
2015-05-13 616
616








