При фиксированном объёме статистических данных качество аппроксимации стохастических зависимостей с помощью непараметрической оценки регрессии существенно зависит от выбранных коэффициентов размытости ядерных функций.
Определение конкретных значений коэффициентов размытости 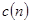 обычно осуществляется из условия минимума эмпирических критериев:
обычно осуществляется из условия минимума эмпирических критериев:
средняя ошибка аппроксимации
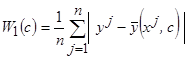 ;
;
среднеквадратическая ошибка аппроксимации
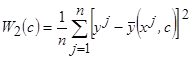 ; (3.12)
; (3.12)
средняя относительная ошибка аппроксимации
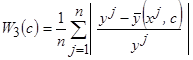 ; (3.13)
; (3.13)
среднеквадратическая относительная ошибка аппроксимации
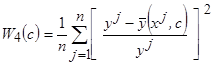 .
.
В преимущество критерия (3.13) состоит в том, что умножив его величину на 100%, получим ошибку аппроксимации в процентном соотношении с диапазоном изменения 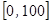 . Иначе говоря, значение критерия не зависит от единиц измерения
. Иначе говоря, значение критерия не зависит от единиц измерения 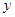 . Основной его недостаток заключается в том, что если
. Основной его недостаток заключается в том, что если 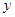 может принимать нулевые значения либо близкие к ним возникает неоднозначность и значения критерия могут значительно превышать 100%.
может принимать нулевые значения либо близкие к ним возникает неоднозначность и значения критерия могут значительно превышать 100%.
В отличие от (3.13) критерий (3.12) может быть использован в любых ситуациях, но его значения зависят от единиц измерения 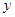 , что затрудняет количественную оценку ошибки аппроксимации.
, что затрудняет количественную оценку ошибки аппроксимации.
Метод скользящего экзамена. Выбор оптимального коэффициента размытости осуществляется по элементам обучающей выборки. Идея метода заключается в том, что последовательно каждая 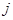 -я точка исходной обучающей выборки принимается в качестве контрольной ситуации с последующим исключением её из процесса обучения. Рассмотрим данный процесс на примере критерия (3.12)
-я точка исходной обучающей выборки принимается в качестве контрольной ситуации с последующим исключением её из процесса обучения. Рассмотрим данный процесс на примере критерия (3.12)
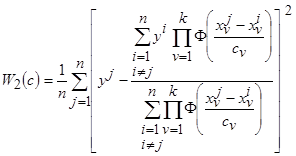 . (3.14)
. (3.14)
Условие 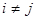 позволяет исключить
позволяет исключить 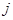 -ю контрольную точку из процесса обучения. При этом оптимальный набор коэффициентов размытости
-ю контрольную точку из процесса обучения. При этом оптимальный набор коэффициентов размытости 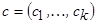 будет соответствовать минимальному значению критерия
будет соответствовать минимальному значению критерия 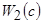
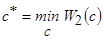 .
.
Для упрощения задачи выбора оптимального коэффициента размытости можно воспользоваться методикой представленной в пункте 2.2.2.2., что позволяет свести задачу оптимизации к нахождению всего лишь одного параметра 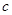 .
.
Рассчитаем по обучающей выборки оценки среднеквадратического отклонения
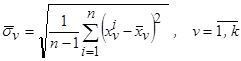 ,
,
которые характеризуют диапазон изменения признаков.
Сопоставим каждому коэффициенту размытости 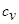 произведение
произведение 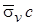 , где неопределённый коэффициент
, где неопределённый коэффициент 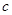 будет общим для каждого признака. В результате получим
будет общим для каждого признака. В результате получим
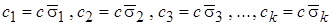 .
.
При этом среднеквадратический критерий (3.14) будет иметь вид
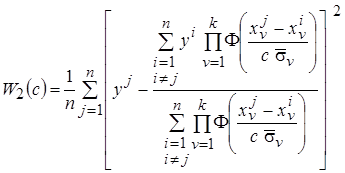 . (3.15)
. (3.15)
Зависимость эмпирического критерия 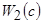 от коэффициента размытости представлена на рис. 3.4.
от коэффициента размытости представлена на рис. 3.4.
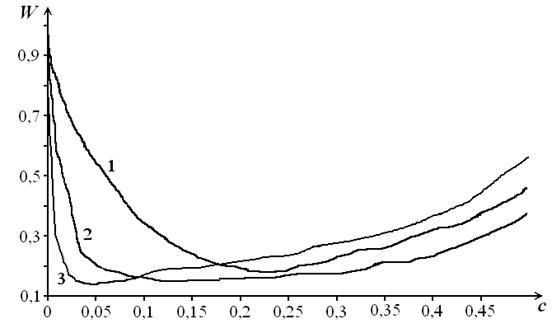
Рис. 3.4. Зависимость ошибки аппроксимации (3.12) от величины коэффициента размытости для одномерного случая (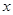 - скаляр).
- скаляр).
Кривая 1 соответствует объёму обучающей выборки 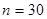 ,
,
кривая 2 - 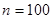 , кривая 3 -
, кривая 3 - 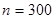 .
.
Метод деления выборки на контрольную и обучающую. Идея метода состоит в декомпозиции исходной обучающей выборки на контрольную 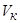 и обучающую
и обучающую 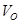 выборки
выборки
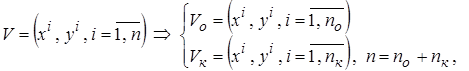
где 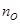 - объём обучающей выборки, а
- объём обучающей выборки, а 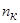 - контрольной.
- контрольной.
При этом среднеквадратический критерий (3.12) будет иметь вид
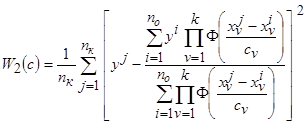 .
.
Данный критерий характеризует среднеквадратическое расхождение между строящейся по выборке 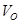 непараметрической регрессией и элементами контрольной выборки
непараметрической регрессией и элементами контрольной выборки 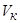 .
.
Рассматриваемый метод поиска оптимального коэффициента размытости наиболее удобно применять при достаточно больших объёмах обучающей выборки (более 200 наблюдений на каждый признак 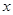 ), когда исследователь может пожертвовать частью исходной выборки
), когда исследователь может пожертвовать частью исходной выборки 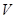 и сформировать контрольную
и сформировать контрольную 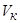 .
.
Метод случайного поиска коэффициентов размытости. Данный метод основан на случайном выборе оптимального вектора 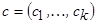 из множества альтернатив, которое генерируется с использованием датчиков случайных величин.
из множества альтернатив, которое генерируется с использованием датчиков случайных величин.
Запишем непараметрическую оценку регрессии (3.5) в виде
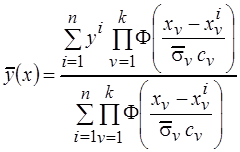 . (3.16)
. (3.16)
Из вычислительных экспериментов установлено, что коэффициенты 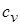 ,
, 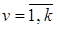 в выражении (3.16) принадлежит интервалу
в выражении (3.16) принадлежит интервалу 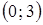 .
.
Для генерации множества векторов 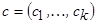 воспользуемся датчиками случайных величин с равномерными законами распределения на интервале
воспользуемся датчиками случайных величин с равномерными законами распределения на интервале 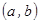
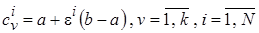 ,
,
где 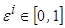 - случайная величина с равномерным законом распределения,
- случайная величина с равномерным законом распределения, 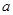 - величина близкая к нулю (например
- величина близкая к нулю (например 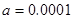 ), а
), а 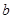 можно принять равным трём. В результате данной операции получим выборку
можно принять равным трём. В результате данной операции получим выборку 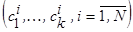 , которую при
, которую при 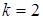 можно отобразить на рис. 3.5.
можно отобразить на рис. 3.5.
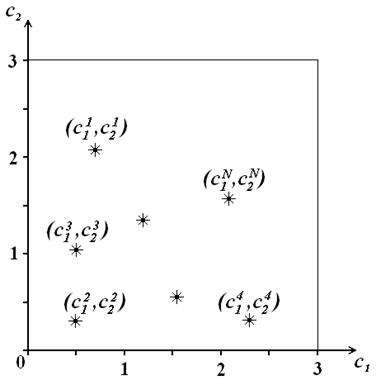
Рис. 3.5. Выборка векторов 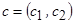 при
при 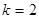 .
.
Последовательно подставляя полученные вектора в среднеквадратический критерий
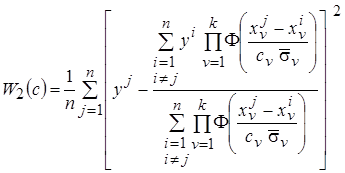 ,
,
получим выборку 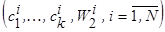 и выберем тот вектор
и выберем тот вектор 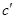 , при котором
, при котором 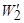 будет минимальна. В окрестности
будет минимальна. В окрестности 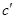 генерируются новые вектора
генерируются новые вектора 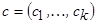 и находится наилучший на данном этапе набор параметров
и находится наилучший на данном этапе набор параметров 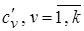 . Описанный процесс продолжается до тех пор пока изменения критерия будут незначительными.
. Описанный процесс продолжается до тех пор пока изменения критерия будут незначительными.
Рандомизированный метод оптимизации непараметрической оценки регрессии. Существующий парадокс традиционных методов идентификации стохастических моделей состоит в сопоставлении случайной выборке наблюдений 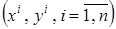 переменных изучаемого объекта конкретного набора параметров модели оптимальных в смысле минимума эмпирической ошибкиаппроксимации. Рассмотрим принципиально новый рандомизированный подход оптимизации непараметрических алгоритмов, основанный на процедуре случайного выбора коэффициентов размытости ядерных функций из некоторой генеральной совокупности с определённым законом распределения. В этом случае непараметрическая оценка регрессии принимает вид
переменных изучаемого объекта конкретного набора параметров модели оптимальных в смысле минимума эмпирической ошибкиаппроксимации. Рассмотрим принципиально новый рандомизированный подход оптимизации непараметрических алгоритмов, основанный на процедуре случайного выбора коэффициентов размытости ядерных функций из некоторой генеральной совокупности с определённым законом распределения. В этом случае непараметрическая оценка регрессии принимает вид
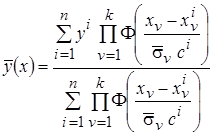 ,
,
где коэффициент размытости 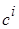 является случайной величиной с плотностью вероятности
является случайной величиной с плотностью вероятности 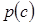 и соответствует наблюдению
и соответствует наблюдению 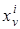 .
.
Из анализа асимптотических свойств непараметрической регрессии следует, что нижняя граница области изменения коэффициента размытости с ростом объёма выборки 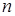 стремится к нулю. Отсюда возникает идея оптимизировать непараметрическую оценку регрессии по виду закона распределения
стремится к нулю. Отсюда возникает идея оптимизировать непараметрическую оценку регрессии по виду закона распределения 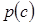
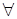
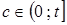 коэффициентов размытости и правой границе
коэффициентов размытости и правой границе 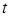 . Для генерации коэффициентов размытости
. Для генерации коэффициентов размытости 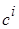 воспользуемся датчиками случайных величин известных законов распределения, например (рис. 3.6):
воспользуемся датчиками случайных величин известных законов распределения, например (рис. 3.6):
Нормальный закон 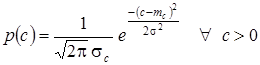 .
.
Равномерный закон 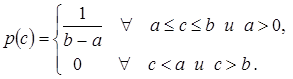
Показательный 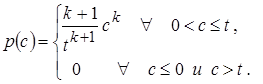
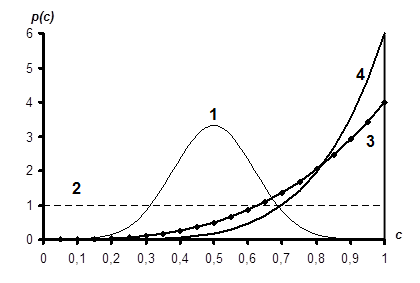
Рис. 3.6. Графики плотностей вероятности в диапазоне 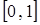 . Кривая 1 соответствует нормальному закону распределения при
. Кривая 1 соответствует нормальному закону распределения при 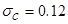 ,
, 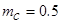 ; кривая 2 – равномерному закону при
; кривая 2 – равномерному закону при 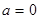 ,
, 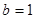 ; кривая 3 и 4 – показательным законам для
; кривая 3 и 4 – показательным законам для 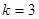 ,
, 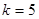 при
при 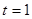 .
.
Воспользуемся результатами раздела 2.5. и сформируем датчики случайных величин введённых законов распределения:
- нормальный закон 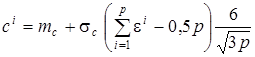 , где параметр распределения
, где параметр распределения 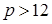 ;
;
- равномерный закон распределения 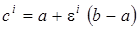 на интервале
на интервале 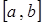 ;
;
- показательный закон распределения 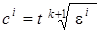 на интервале
на интервале 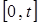 .
.
Здесь 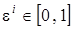 случайная величина с равномерным законом распределения.
случайная величина с равномерным законом распределения.
При использовании датчика случайных значений коэффициентов размытости с нормальным законом распределения задача оптимизации непараметрической оценки регрессии сводится к нахождению оптимальных значений математического ожидания коэффициента размытости 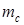 и его среднеквадратического отклонения
и его среднеквадратического отклонения 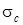 . Для датчика с равномерным законом необходимо определить оптимальную длину интервала
. Для датчика с равномерным законом необходимо определить оптимальную длину интервала 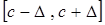 , (
, (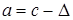 и
и 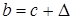 ) и его центр, а при использовании датчика с показательным законом необходимо эффективно оценить правую границу
) и его центр, а при использовании датчика с показательным законом необходимо эффективно оценить правую границу 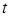 и наилучшую степень
и наилучшую степень 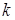 .
.
При использовании датчика случайных чисел, например, с показательным законом распределения при 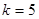 непараметрическая оценка регрессии имеет вид
непараметрическая оценка регрессии имеет вид
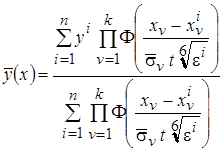 , (3.17)
, (3.17)
где оптимальный набор параметров 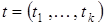 определяется из эмпирической оценки среднеквадратического отклонения
определяется из эмпирической оценки среднеквадратического отклонения
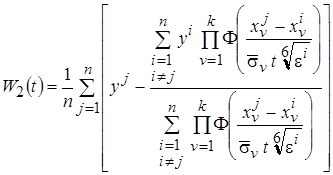 .
.
Пример применения непараметрической оценки регрессии при восстановлении стохастической зависимости. Для иллюстрации эффективности непараметрической оценки регрессии (3.4) в задачах восстановления стохастических зависимостей (3.1) проведён вычислительный эксперимент с использованием функции
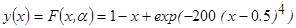 . (3.18)
. (3.18)
Методика формирования исходных данных:
1. Случайная величина 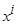 генерировалась в диапазоне
генерировалась в диапазоне 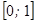 с равномерным законом распределения.
с равномерным законом распределения.
2. Значения функции 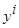 получались путём подстановки
получались путём подстановки 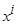 в полином (3.18)
в полином (3.18)
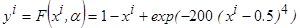 .
.
3. Полученная выборка 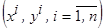 зашумлялась, накладывая на значения восстанавливаемой функции аддитивную относительную помеху
зашумлялась, накладывая на значения восстанавливаемой функции аддитивную относительную помеху
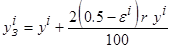 ,
,
где 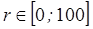 - уровень шума,
- уровень шума, 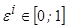 - случайная величина с равномерным законом распределения.
- случайная величина с равномерным законом распределения.
Используя непараметрическую оценку регрессии (3.4) и метод скользящего экзамена при её оптимизации по данным 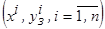 восстанавливалась зависимость
восстанавливалась зависимость 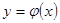 рис. 3.7.
рис. 3.7.
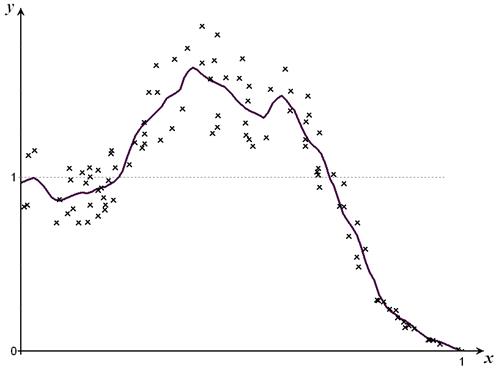
Рис. 3.7. Иллюстрация восстановления стохастической зависимости (3.1) с помощью непараметрической регрессии(3.4) при 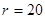 ,
, 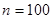 .
.
 2015-05-13
2015-05-13 2222
2222








