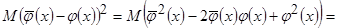
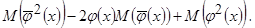
Рассмотрим отдельно второе и третье слагаемое:
1). Подставим в удвоенное произведение выражение (3.8), тогда
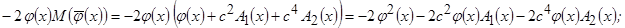
2). 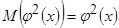 ;
;
Рассмотрим первое слагаемое
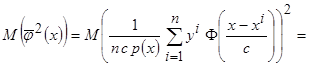
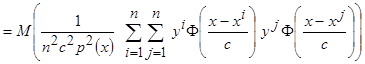 .
.
Двойную сумму можно представить в виде квадратной матрицы с 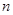 - столбцами и
- столбцами и 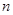 - строками. Выделим главную диагональ матрицы
- строками. Выделим главную диагональ матрицы 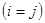 и все остальные элементы
и все остальные элементы
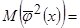
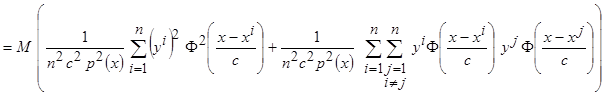 .
.
(3.9)
Рассмотрим данное выражение (3.9) по частям, сначала слагаемое соответствующее главной диагонали матрицы
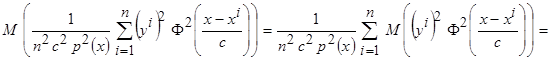
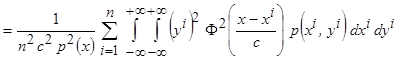 .
.
Учитывая, что 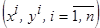 наблюдения одной и той же случайной величины
наблюдения одной и той же случайной величины 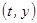 , поэтому
, поэтому 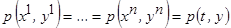 .
.
Тогда
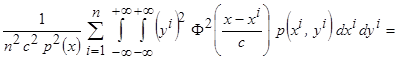
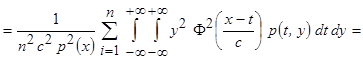
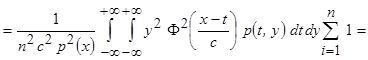
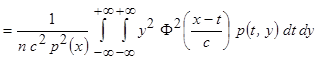 .
.
Представим совместную плотность вероятности 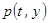 в виде произведения
в виде произведения 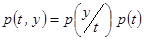 и выделив квадрат условного математического ожидания
и выделив квадрат условного математического ожидания 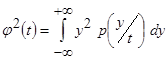 , получаем
, получаем
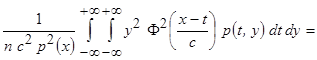
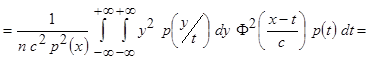
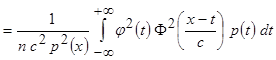 .
.
После замены переменных 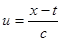 ,
, 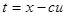 ,
, 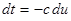 и т.д., получаем
и т.д., получаем
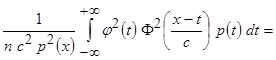
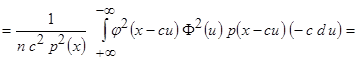
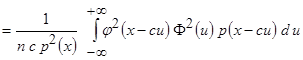 .
.
Разложим функции 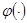 и
и 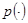 в ряд Тейлора в точке
в ряд Тейлора в точке 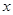 до второй производной. Тогда
до второй производной. Тогда
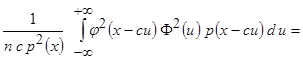
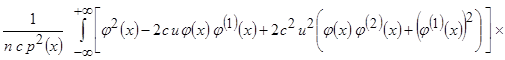
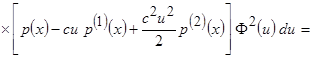
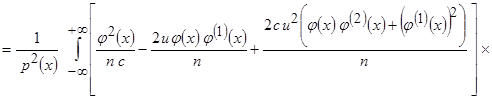
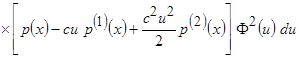 .
.
Заметим, что 3-е слагаемое в первой скобки содержит отношение 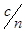 . Если
. Если 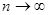 , а
, а 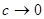 , то отношение
, то отношение 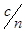 очень мало. Поэтому для упрощения дальнейших выкладок будем пренебрегать ими. Тогда получим
очень мало. Поэтому для упрощения дальнейших выкладок будем пренебрегать ими. Тогда получим
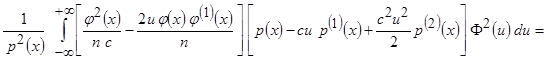
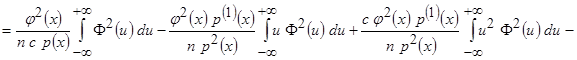
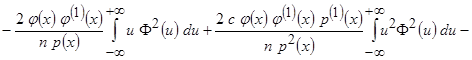
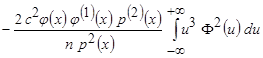 .
.
Так как 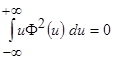 и
и 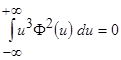 , а слагаемыми с коэффициентом
, а слагаемыми с коэффициентом 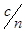 несоизмеримо малы, то выражение, соответствующее элементам главной диагонали матрицы имеет вид
несоизмеримо малы, то выражение, соответствующее элементам главной диагонали матрицы имеет вид
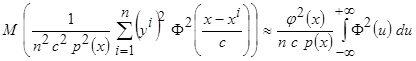 .
.
Рассмотрим второе слагаемое выражения (3.9)
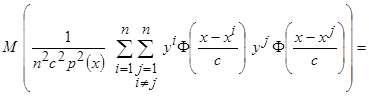
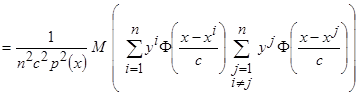 .
.
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, поэтому данное выражение принимает вид
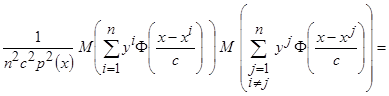
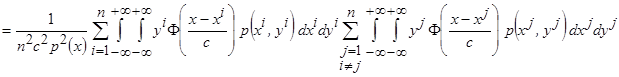 .
.
Учитывая, что 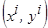 и
и 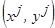 наблюдения одной и той же случайной величины
наблюдения одной и той же случайной величины 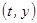 , тогда
, тогда 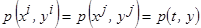 .
.
Тогда
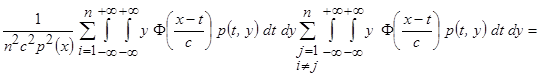
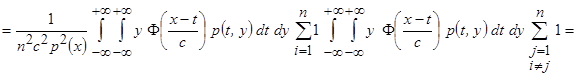
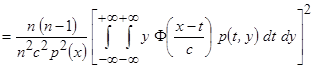 .
.
При 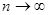 отношение
отношение 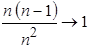 . Внесём
. Внесём 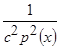 под квадрат, а совместную плотность вероятности
под квадрат, а совместную плотность вероятности 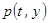 представим в виде произведения
представим в виде произведения 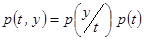 , получим
, получим
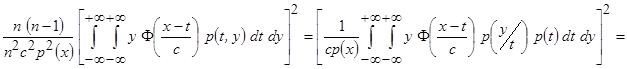
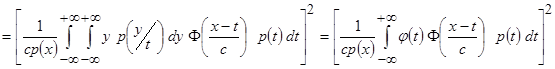 .
.
Заметим, что полученное выражение соответствует квадрату математического ожидания 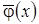
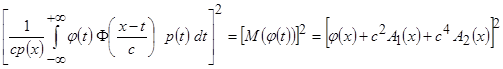 .
.
Раскрывая квадрат и пренебрегая слагаемыми малости 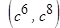 , получим
, получим
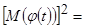
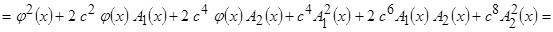
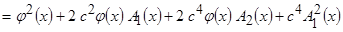 .
.
В итоге выражение, соответствующее среднеквадратическому отклонению, имеет вид
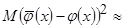
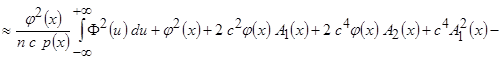
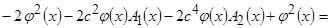
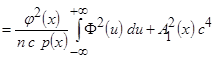 .
.
Вычислим интегральное выражение среднеквадратического отклонения
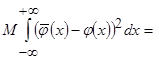
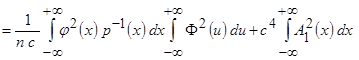 . (3.10)
. (3.10)
Оптимальный коэффициент размытости, минимизирующее интегральное среднеквадратическое отклонение
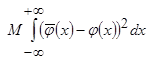 ,
,
определяется по формуле
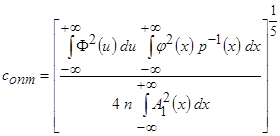 . (3.11)
. (3.11)
Из полученного выражения следует, что 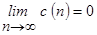 .
.
 2015-05-13
2015-05-13 730
730








