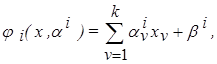2015-05-13
498
(3.21)
где параметры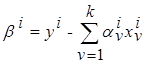 
, а коэффициенты 
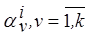находятся из условия минимума критерия
.
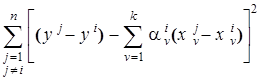Тогда задача определения параметров может быть сведена к решению системы линейных уравнений
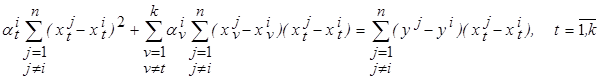
относительно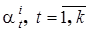 
, используя, например, правило Крамера либо метод Гаусса.
Например, при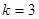 
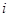-я линейная опорная функция имеет вид
,
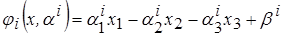а система уравнений для определения её коэффициентов (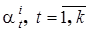) представляется в матричном виде
, 
,
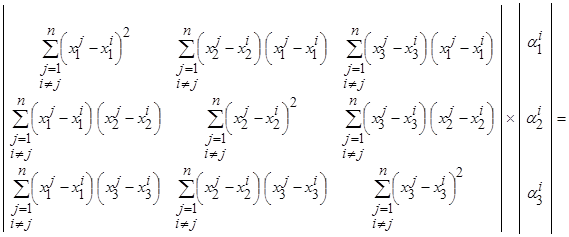
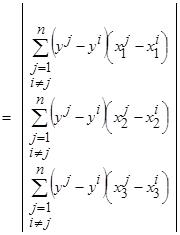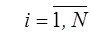где свободный член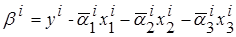 
.
В одномерном случае, когда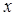 
является скаляром, значения
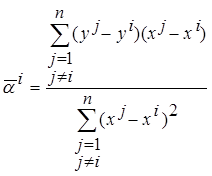. (3.22)
С целью уменьшения количества опорных аппроксимаций целесообразно усложнить их вид.
