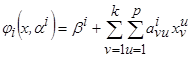Для нелинейных опорных функций

, (3.23)

где 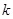- количество признаков вектора входной переменной 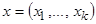, 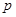- максимальная степень опорной аппроксимации.

Исходя из условия прохождения опорной аппроксимации через опорную точку параметр 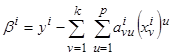, а коэффициенты 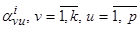находятся из условия минимума критерия

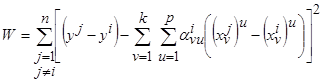. (3.24)

В одномерном случае (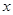 - скаляр), при максимальной степени опорной аппроксимации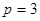

.

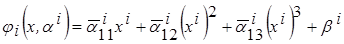Задача определения коэффициентов сводится к нахождению минимума критерия

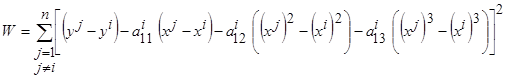
путём решения системы уравнений с помощью правила Крамера либо метода Гаусса

, ,

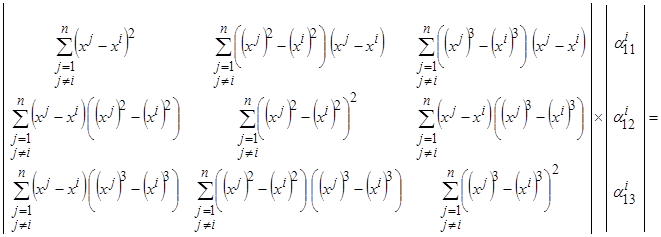
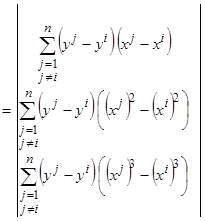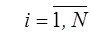где свободный член .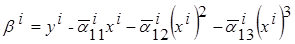

Для многомерного случая задача определения параметров нелинейной опорной функции может быть сведена к решению системы линейных уравнений ()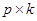

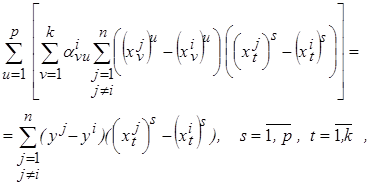
относительно .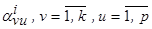

Объединение упрощённых параметрических аппроксимаций в коллектив осуществляется на основе процедуры условного усреднения

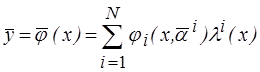, (3.25)

где положительная, ограниченная значением единица функция 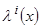определяет «вес» правила 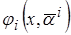при формировании решения в ситуации .

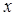Примером функции 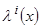является нормированное расстояние между точками 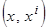(основанная на преобразовании Евклидовых расстояний)

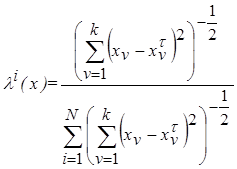
либо «весовая» функция

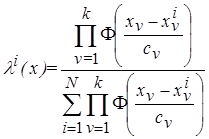, (3.26)

составленная из «ядерных» функций 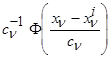, на основе которых строятся непараметрические модели.