2015-05-13
630
Структуру предлагаемых моделей составляют семейство упрощённых параметрических аппроксимаций искомой зависимости, не имеющих самостоятельного значения, которые строятся относительно системы «опорных» ситуаций из обучающей выборки. Объединение упрощённых аппроксимаций в коллектив реализуется с помощью непараметрической оценки оператора условного математического ожидания.
Пусть дана выборка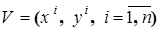 
из статистически независимых наблюдений значений неизвестной функции
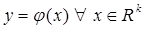(3.19)
и её аргументов.
Преобразование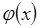 
и плотности вероятности 
, 
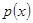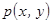достаточно гладкие и имеют хотя бы первые две производные.
Поставим в соответствие некоторым точкам обучающей выборки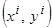 
, условно назовём их «опорными»,упрощённые параметрические аппроксимации 
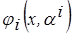(опорные функции) зависимости (3.19), параметры которых удовлетворяют условиям
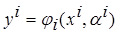, (3.20)
, 
,
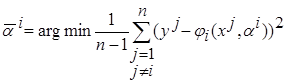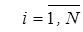т.е.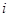 
-я упрощённая аппроксимация проходит через 
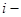ю «опорную» точку и близка с среднеквадратическом ко всем остальным элементам обучающей выборки.
Здесь и далее опорные точки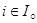 
, выбираемые из выборки 
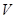, упорядочиваются 
.
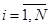Упрощенные параметрические аппроксимации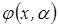 
могут быть линейными либо нелинейными.
