Используем линейные опорные аппроксимации (3.21) в коллективной модели (3.25) при весовой функции 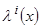 (3.26). Рассчитаем коэффициент
(3.26). Рассчитаем коэффициент 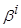 из условия прохождения упрощённой аппроксимации
из условия прохождения упрощённой аппроксимации 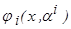 через
через 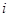 -ю опорную точку
-ю опорную точку
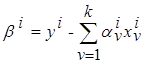 .
.
Подставим полученное выражение 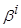 в опорную аппроксимацию (3.21). В результате имеем
в опорную аппроксимацию (3.21). В результате имеем
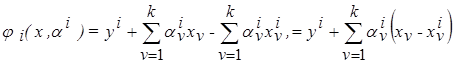 . (3.27)
. (3.27)
Полученную опорную аппроксимацию подставим в коллектив (3.25)
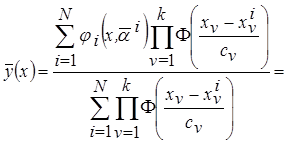
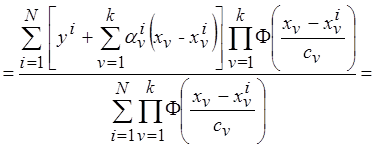
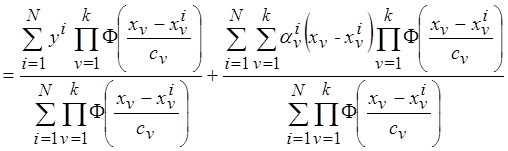 .
.
Несложно заметить, что непараметрическая модель коллективного типа (3.25) при линейных опорных функциях допускает представление в виде двух слагаемых
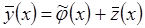 ,
,
где первое слагаемое 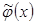 является непараметрической регрессией (3.5), построенной по опорным точкам, а второе
является непараметрической регрессией (3.5), построенной по опорным точкам, а второе 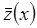 - играет роль поправочного члена и отражает условную взаимосвязь между точками обучающей выборки, значения которого снижаются по мере роста объёма исходной информации. Причём, если линейные опорные функции будут проходить параллельно оси
- играет роль поправочного члена и отражает условную взаимосвязь между точками обучающей выборки, значения которого снижаются по мере роста объёма исходной информации. Причём, если линейные опорные функции будут проходить параллельно оси 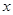 , что будет соответствовать
, что будет соответствовать 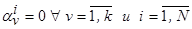 , тогда второе слагаемое
, тогда второе слагаемое 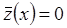 , а
, а 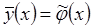 .
.
 2015-05-13
2015-05-13 681
681








