Проблема оптимизации непараметрических моделей коллективного типа охватывает определение рационального закона распределения «опорных» точек, выбор оптимальных коэффициентов размытости и ядерных функций.
Выбор оптимальной ядерной функции осуществляется по аналогии с пунктом 3.3.2. При этом установлено, что оптимальным с смысле минимума среднеквадратического отклонения является ядро Епанечникова
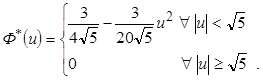
Оптимизация непараметрических моделей коллективного типа осуществляется по аналогии с непараметрической оценкой регрессией (пункт 3.3.3).
Выбор закона распределения опорных точек. Выбор рационального закона распределения опорных точек осуществляется, основываясь на основных положениях теории вероятностей, путем решения следующей вариационной задачи

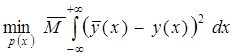 ,
,
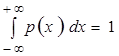 ,
,
где 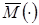 - асимптотическое выражение среднеквадратического критерия (3.31).
- асимптотическое выражение среднеквадратического критерия (3.31).
В соответствии с результатами решения данной задачи рекомендуется выбирать «опорные» точки с законом распределения
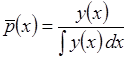
повторяющим вид восстанавливаемой зависимости, что позволяет минимизировать главную составляющую дисперсии 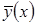 . При этом большая часть «опорных» точек формируется в области больших значений восстанавливаемой функции и её производных.
. При этом большая часть «опорных» точек формируется в области больших значений восстанавливаемой функции и её производных.
Итерационная процедура формирования упрощённых аппроксимаций. Пусть 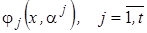 - некоторая система
- некоторая система 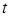 упрощённых аппроксимаций зависимости
упрощённых аппроксимаций зависимости 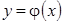 построенная относительно «опорных» точек
построенная относительно «опорных» точек 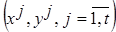 . При этом эмпирическая ошибка расхождения между экспериментальными данными и строящейся непараметрической моделью
. При этом эмпирическая ошибка расхождения между экспериментальными данными и строящейся непараметрической моделью 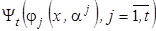
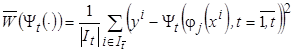 ,
,
где 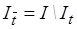 - множество номеров точек не входящих в число «опорных»
- множество номеров точек не входящих в число «опорных» 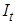 ;
; 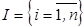 - множество номеров точек исходной выборки.
- множество номеров точек исходной выборки.
Вклад слагаемых в формирование эмпирической ошибки неравнозначный. Если модель 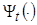 в некоторой точке
в некоторой точке 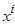 имеет максимальное расхождение с экспериментальным значением
имеет максимальное расхождение с экспериментальным значением 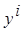 , то естественно было бы принять точку
, то естественно было бы принять точку 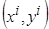 в качестве «опорной» при построении
в качестве «опорной» при построении 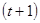 -ой упрощённой аппроксимации. Однако существующая невязка может быть связана с ошибкой системы контроля. Для проверки данной гипотезы можно воспользоваться условием непрерывности: близким значениям аргумента соответствуют близкие значения функции.
-ой упрощённой аппроксимации. Однако существующая невязка может быть связана с ошибкой системы контроля. Для проверки данной гипотезы можно воспользоваться условием непрерывности: близким значениям аргумента соответствуют близкие значения функции.
Методика формирования системы «опорных» точек модели представляется следующей последовательностью действий:
1. Выбрать в качестве первой «опорной» 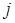 -юточку с максимальным значением функции либо её производной. Принять значение параметра
-юточку с максимальным значением функции либо её производной. Принять значение параметра 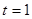 .
.
2. Включить номер 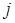 -й «опорной» точки в множество
-й «опорной» точки в множество 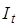 .
.
3. Оценить параметры упрощённой параметрической аппроксимации 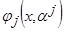 .
.
4. Построить непараметрическую модель коллективного типа 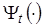 .
.
5. Проверить соответствие количества опорных точек 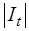 требуемому
требуемому 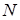 либо заданной оценке точности аппроксимации. Если условие выполнено, то процесс заканчивается.
либо заданной оценке точности аппроксимации. Если условие выполнено, то процесс заканчивается.
6. Определить новую опорную точку 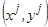 из условия
из условия
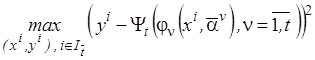 .
.
Принять 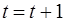 и перейти к этапу 2.
и перейти к этапу 2.
Комбинированная процедура формирования упрощённых аппроксимаций. В процессе исследований непараметрических моделей коллективного типа возникла идея создания метода формирования упрощённых аппроксимаций, учитывающих преимущество рационального метода и итерационной процедуры формирования опорных точек. Итерационная процедура обусловлена значительными временными затратами, а рациональный закон распределения сложен в реализации. Поэтому предлагается комбинированная процедура формирования упрощённых аппроксимаций.
Идея предлагаемого подхода формирования последовательности опорных точек основывается на их моделировании с равномерными законом распределения и последующей доводкой с помощью итерационной процедуры выбора упрощённых аппроксимаций, минимизирующих на каждом этапе относительную эмпирическую ошибку между восстанавливаемой зависимостью и её коллективной моделью.
Предлагаемая методика:
1. Выбрать из обучающей выборки 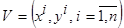 с помощью датчика случайных чисел
с помощью датчика случайных чисел 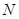 опорных точек
опорных точек 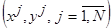 .
.
2. Оценить оптимальные параметры моделей 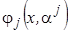 из условия
из условия
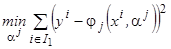 ,
,
где 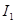 - множество номеров точек не входящих в число опорных.
- множество номеров точек не входящих в число опорных.
3. Построить непараметрическую модель коллективного типа
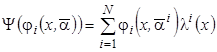 ,
,
где 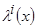 - нормированное расстояние между точками
- нормированное расстояние между точками 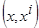 либо ядерная функция.
либо ядерная функция.
4. Определить следующую опорную точку 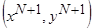 из условия
из условия
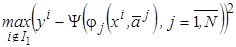 .
.
5. Оценить оптимальные параметры модели 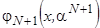
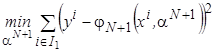 .
.
Далее принять 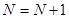 и перейти к этапу 3. Так продолжать до тех пор, пока ошибка восстановления не будет удовлетворять пользователя.
и перейти к этапу 3. Так продолжать до тех пор, пока ошибка восстановления не будет удовлетворять пользователя.
 2015-05-13
2015-05-13 552
552








