2015-05-13
808
Для удобства последующего анализа предположим, что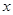 
- скаляр и закон распределения 
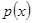известен, а опорные функции 
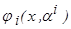- линейные. Тогда непараметрическая модель коллективного типа принимает вид
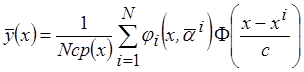(3.28)
Запишем оценку непараметрической модели коллективного типа (3.28) с учётом выражения (3.27) в виде статистики
,
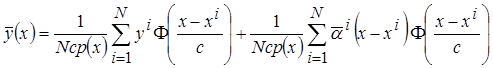которая позволяет упростить методику исследования асимптотических свойств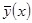 
.
Теорема 3.2. Пусть: 1)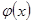 
и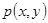 
, 
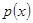в области определения 
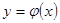ограничены и непрерывны со всеми своими производными до второго порядка включительно; 2) ядерные функции 
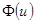являются положительными, нормированными и симметричными, а также 
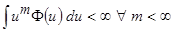; 3) последовательность 
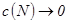при 
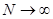, а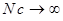 
. Тогда непараметрическая модель коллективного типа 
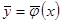обладает свойствами асимптотической несмещённости и состоятельности.
Асимптотические выражения смещения оценки (3.28) и её среднеквадратического отклонения после стандартных аналитических преобразований принимают вид
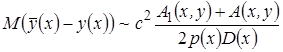, (3.29)
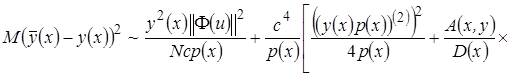
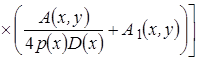, (3.30)
где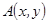 
, 
- нелинейные функционалы от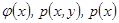 
и их производных; 
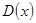- дисперсия опорных точек; 
.
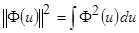Из асимптотических выражений (3.29), (3.30) пр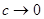и 
и 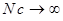следует асимптотическая несмещённость и сходимость в среднеквадратическом непараметрической модели коллективного типа .
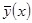Установлено, что асимптотические свойства непараметрических моделей коллективного типа «слабо» зависят от вида упрощённых аппроксимаций и объёма выборки в задаче их идентификации. Эффективность рассматриваемых моделей в значительной степени определяется законом распределения системы опорных точек и их количеством.
Данные выводы подтверждает выражение минимального среднеквадратического отклонения при оптимальном значении параметра размытости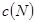 
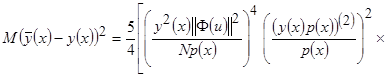
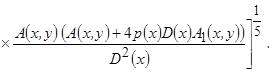(3.31)
