По I закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле электрической цепи, равна нулю, т.е.
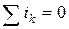 .
.
В соответствии с теоремой о сумме I закон Кирхгофа в символической или комплексной форме записывается в виде
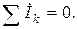 (3.31)
(3.31)
По II закону Кирхгофа алгебраическая сумма мгновенных значений падений напряжений в замкнутом контуре равна нулю, т.е.
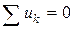 или
или 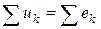 или
или 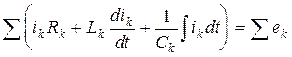 . (3.32)
. (3.32)
Но в соответствии с теоремами символического метода II закон Кирхгофа в символической или комплексной форме записи имеет следующий вид:
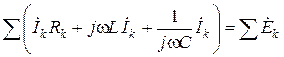 или
или 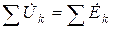 . (3.33)
. (3.33)
Рассмотрим закон Ома в символической форме записи для элементов цепи гармонического тока (рис. 3.15).
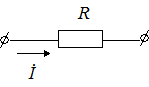 | 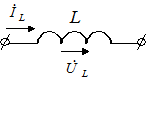 | 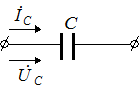 |
Если 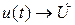 , , 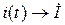 (по теореме о линейном преобразовании), то (по теореме о линейном преобразовании), то 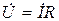 . Это закон Ома в символической форме. . Это закон Ома в символической форме. |  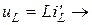 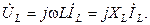 (по теореме о производной) Закон Ома: (по теореме о производной) Закон Ома: 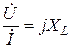 . . | 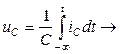 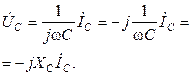 (по теореме об интеграле) Закон Ома: (по теореме об интеграле) Закон Ома: 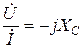 . . |
На рис. 3.16 приведены векторные диаграммы напряжений и токов соответственно для сопротивления, индуктивности и емкости.
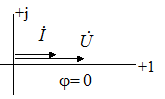 |  | 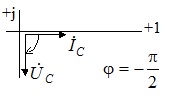 |
3.3.3. Последовательное соединение R, L, C
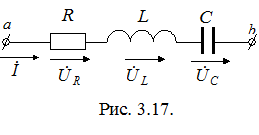 По II закону Кирхгофа
По II закону Кирхгофа
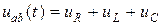 .
.
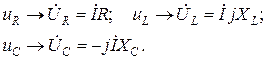
На основании теоремы о сумме
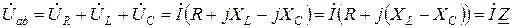 , (3.34)
, (3.34)
где 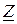 – комплексное сопротивление цепи.
– комплексное сопротивление цепи.
На основании теоремы Эйлера
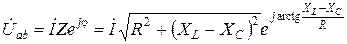 . (3.35)
. (3.35)
Полное сопротивление равно модулю полного комплексного сопротивления 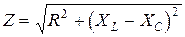 , аргумент полного комплексного сопротивления равен разности фаз напряжения и тока
, аргумент полного комплексного сопротивления равен разности фаз напряжения и тока 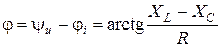 .
.
Комплексное сопротивление можно представить в виде
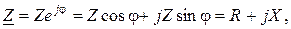 (3.36)
(3.36)
где R – действительная часть комплексного сопротивления, называется активным сопротивлением, 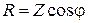 ;
;
X – мнимая часть комплексного сопротивления, называется реактивным сопротивлением, 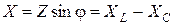 .
.
Таким образом, закон Ома в общем виде 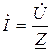 , где
, где 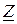 может представлять, в частности, следующее: для сопротивления
может представлять, в частности, следующее: для сопротивления 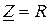 , для индуктивности
, для индуктивности 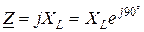 , для емкости
, для емкости 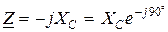 .
.
Введем понятие комплексной проводимости 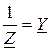 . (3.37)
. (3.37)
Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является ток, вектор тока и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.18).
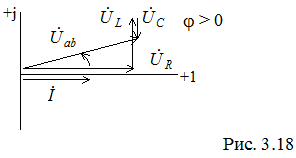 | 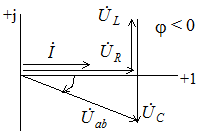 |
Возможны три режима работы такой цепи:
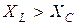 – индуктивный режим,
– индуктивный режим, 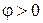 ;
;
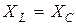 – резонанс напряжений,
– резонанс напряжений, 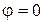 ;
;
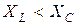 – емкостный режим,
– емкостный режим, 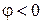 .
.
Угол j(разность начальных фаз напряжения и тока) определяется углом поворота вектора тока к вектору напряжения по кратчайшему пути: если поворот определяется против часовой стрелки, то 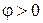 (отстающий ток), иначе –
(отстающий ток), иначе – 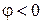 (опережающий ток). Как видно из приведенных выше формул, характер цепи определяет большее реактивное сопротивление.
(опережающий ток). Как видно из приведенных выше формул, характер цепи определяет большее реактивное сопротивление.
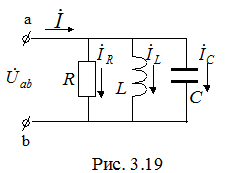
3.3.4. Параллельное соединение R, L, C
Пусть к цепи, состоящей из параллельного соединения R, L, C элементов (рис. 3.19), приложено напряжение 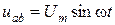 , которому соответствует
, которому соответствует 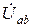 . Определим токи во всех ветвях.
. Определим токи во всех ветвях.
 По I закону Кирхгофа мгновенное значение тока
По I закону Кирхгофа мгновенное значение тока
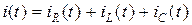 .
.
Согласно теореме о сумме
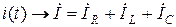 .
.
Применим для каждой ветви закон Ома в комплексной форме:
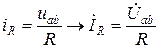 ,
,
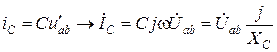 ,
,
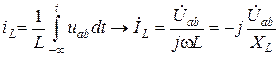 .
.
Тогда 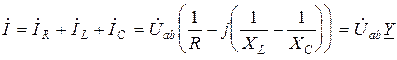 , (3.38)
, (3.38)
где 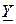 – полная комплексная проводимость
– полная комплексная проводимость 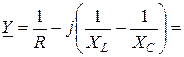
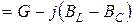 ;
;
активная проводимость 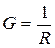 ;
;
индуктивная проводимость 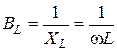 ;
;
емкостная проводимость 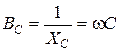 .
.
На основании формулы Эйлера
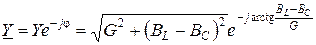 . (3.39)
. (3.39)
Действительная часть комплексной проводимости 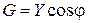 , называется активной проводимостью;
, называется активной проводимостью;
мнимая часть комплексной проводимости 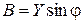 , называется реактивной проводимостью.
, называется реактивной проводимостью.
Для рассматриваемой цепи построим векторную диаграмму токов и напряжений. Поскольку для всех элементом общим является напряжение 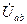 , вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).
, вектор напряжения и выберем в качестве исходного вектора, направив его по действительной оси (рис. 3.20).
 |  |
Возможны три режима работы такой цепи:
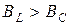 – индуктивный режим,
– индуктивный режим, 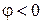 ;
;
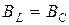 – резонанс токов,
– резонанс токов, 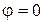 ;
;
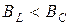 – емкостный режим,
– емкостный режим, 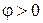 .
.
Таким образом, в параллельных ветвях характер цепи определяет большая реактивная проводимость или меньшее реактивное сопротивление.
 2015-05-13
2015-05-13 1229
1229
