Интеграл от аналитической функции обладает замечательным свойством, сформулированным в теореме Коши.
Теорема Коши. Если 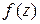 – однозначная аналитическая функция в односвязной области
– однозначная аналитическая функция в односвязной области 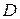 , то интеграл от этой функции по любому замкнутому контуру
, то интеграл от этой функции по любому замкнутому контуру 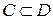 равен нулю:
равен нулю:
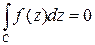 (1)
(1)
Другими словами, интеграл от однозначной аналитической функции в односвязной области не зависит от пути интегрирования.
Пример 1. Интеграл 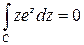 по любой замкнутой кривой
по любой замкнутой кривой  , так как функция
, так как функция 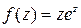 является аналитической на всей комплексной плоскости.?
является аналитической на всей комплексной плоскости.?
Задача 1. Дана функция 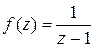 . Можно ли применить теорему Коши к интегралу
. Можно ли применить теорему Коши к интегралу 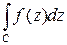 , если а)
, если а) 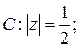 б)
б) 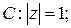 в)
в) 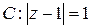 . Ответ аргументируйте. Ответ: 1) можно; 2) нельзя; 3) нельзя.
. Ответ аргументируйте. Ответ: 1) можно; 2) нельзя; 3) нельзя.
В качестве положительного направления обхода замкнутого контура принимается направление, при котором область, ограниченная этим контуром, остается слева.
Так, если контур 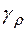 представляет собой окружность
представляет собой окружность 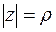 , то
, то 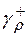 (против часовой стрелки) есть граница круга
(против часовой стрелки) есть граница круга 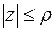 , а
, а 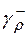 (по часовой стрелке) есть граница внешности круга, то есть области
(по часовой стрелке) есть граница внешности круга, то есть области 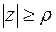 .
.
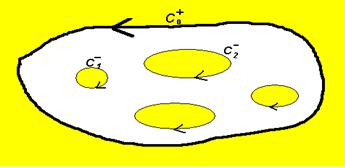
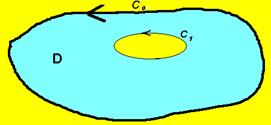
В случае многосвязной области (рис.1) ее полная граница состоит из внешнего контура 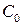 и внутренних контуров
и внутренних контуров 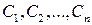 . При положительном направлении обхода полной границы область все время остается слева, т. е. внешний контур обходится против часовой стрелки, а каждый внутренний – по часовой стрелке.
. При положительном направлении обхода полной границы область все время остается слева, т. е. внешний контур обходится против часовой стрелки, а каждый внутренний – по часовой стрелке.
Рис.1
Теорема Коши для многосвязной области.
Пусть 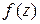 – аналитическая функция в многосвязной области
– аналитическая функция в многосвязной области 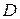 с полной границей
с полной границей 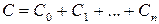 и непрерывна в замкнутой области
и непрерывна в замкнутой области 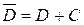 . Тогда интеграл от функции
. Тогда интеграл от функции 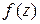 по полной границе
по полной границе  области
области 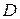 равен нулю (обход границы совершается в положительном направлении):
равен нулю (обход границы совершается в положительном направлении):
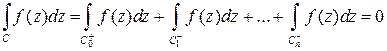 (2)
(2)
Формулу (2) можно переписать в виде:
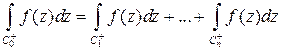 (3)
(3)
Значит, интеграл от функции 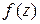 по внешнему контуру
по внешнему контуру 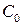 равен сумме интегралов по внутренним контурам
равен сумме интегралов по внутренним контурам 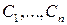 (каждый из контуров обходится против часовой стрелки).
(каждый из контуров обходится против часовой стрелки).
В частности, пусть функция 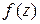 является аналитической на контурах
является аналитической на контурах 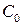 ,
, 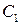 и в двухсвязной области
и в двухсвязной области 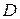 , ограниченной этими Рис.2
, ограниченной этими Рис.2
контурами (рис.2). Тогда из (3) получаем
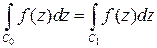 . (4)
. (4)
В этом случае интеграл независимо от формы кривой интегрирования сохраняет постоянное значение.
Пример 2. Показать, что если  произвольный замкнутый контур, не проходящий через точку
произвольный замкнутый контур, не проходящий через точку  , и
, и 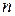 – целое число, то
– целое число, то
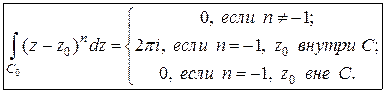
Решение. При 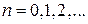 подынтегральная функция
подынтегральная функция 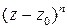 является аналитической и интеграл равен нулю в силу теоремы Коши (независимо от взаимного расположения точки
является аналитической и интеграл равен нулю в силу теоремы Коши (независимо от взаимного расположения точки  и контура
и контура  ).
).
При 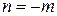 подынтегральная функция имеет вид
подынтегральная функция имеет вид 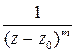 , где
, где 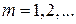 Пусть точка
Пусть точка  находится вне контура
находится вне контура  , тогда функция
, тогда функция 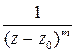 является аналитической внутри этого контура. И в этом случае справедлива теорема Коши – интеграл равен нулю.
является аналитической внутри этого контура. И в этом случае справедлива теорема Коши – интеграл равен нулю.
Осталось рассмотреть интеграл 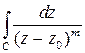 , когда точка
, когда точка  находится внутри контура
находится внутри контура  , то есть в точке
, то есть в точке  нарушается аналитичность подынтегральной функции. Выбросим из области круг
нарушается аналитичность подынтегральной функции. Выбросим из области круг 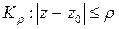 , граница
, граница 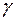 которого лежит внутри контура
которого лежит внутри контура  . Функция
. Функция 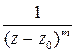 аналитична и на контуре
аналитична и на контуре  , и на окружности
, и на окружности 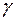 , а также в двухсвязной области, ограниченной этими контурами. Значит, интеграл в силу формулы (1) сохраняет постоянное значение, которое можно найти, принимая за контур интегрирования окружность
, а также в двухсвязной области, ограниченной этими контурами. Значит, интеграл в силу формулы (1) сохраняет постоянное значение, которое можно найти, принимая за контур интегрирования окружность 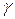 :
: 
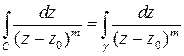 .
.
В примере 3 предыдущего параграфа было показано, что такой интеграл не зависит ни от радиуса 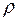 окружности, ни от точки
окружности, ни от точки  , интеграл равен нулю при
, интеграл равен нулю при 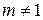 и равен
и равен 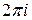 при
при 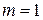 . Все возможные случаи исчерпаны.?
. Все возможные случаи исчерпаны.?
Аналитичность функции налагает на нее такие жесткие условия, что информации о поведении функции на некоторой замкнутой кривой в области аналитичности достаточно, чтобы определить значение функции в любой внутренней точке области – этот факт отражен в интегральной формуле Коши.
Интегральная формула Коши
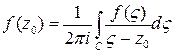 (5)
(5)
позволяет вычислить значение функции 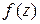 в любой точке
в любой точке  области ее аналитичности
области ее аналитичности 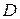 , если известны значения
, если известны значения 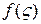 этой функции на контуре
этой функции на контуре  , целиком лежащем в
, целиком лежащем в 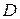 и содержащем внутри себя точку
и содержащем внутри себя точку  .
.
Интеграл, стоящий справа в формуле Коши, называется интегралом Коши.
В подынтегральном выражении 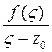 первый множитель
первый множитель 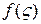 – это плотность интеграла Коши (значение на контуре
– это плотность интеграла Коши (значение на контуре  функции
функции 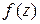 , аналитической всюду в
, аналитической всюду в 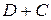 , во всяком случае, непрерывной на контуре
, во всяком случае, непрерывной на контуре  ). Второй множитель
). Второй множитель 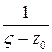 – это ядро интеграла Коши (значение на контуре
– это ядро интеграла Коши (значение на контуре  функции
функции 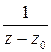 , которая теряет аналитичность в точке
, которая теряет аналитичность в точке 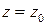 , если
, если 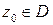 и является аналитической всюду в
и является аналитической всюду в 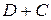 , если точка
, если точка  находится вне контура
находится вне контура  ).
).
Значит, интеграл Коши равен
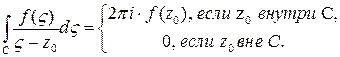 (6)
(6)
Заметим, что в задачах обычно не подчеркивается разница между переменной интегрирования 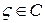 и точкой
и точкой 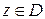 .
.
Пример 3. Вычислить интеграл 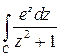 , где контур
, где контур 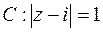 .
.
Решение. Подынтегральная функция 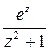 имеет две особые точки:
имеет две особые точки: 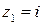 и
и 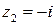 . Первая из них лежит внутри заданного контура интегрирования, а вторая – вне его.
. Первая из них лежит внутри заданного контура интегрирования, а вторая – вне его.
Представим интеграл в виде:
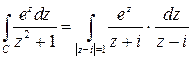 .
.
Здесь в подынтегральной функции 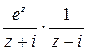 множитель
множитель 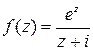 представля-
представля-
ет собой аналитическую внутри контура  и на нем функцию – это плотность интеграла Коши. Множитель
и на нем функцию – это плотность интеграла Коши. Множитель 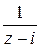 – ядро интеграла Коши (аналитичность нарушается во внутренней точке
– ядро интеграла Коши (аналитичность нарушается во внутренней точке 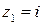 ). Согласно формуле (6)
). Согласно формуле (6)
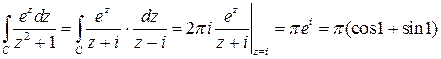 .?
.?
Задача 2. Вычислить интеграл 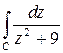 , если а) точка
, если а) точка 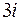 лежит внутри контура
лежит внутри контура  , а точка
, а точка 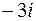 вне его; б) точка
вне его; б) точка 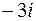 лежит внутри контура
лежит внутри контура  , а точка
, а точка 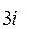 вне его; в) обе особые точки лежат вне контура
вне его; в) обе особые точки лежат вне контура  . Ответ: а)
. Ответ: а) 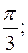 б)
б) 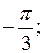 в) 0.
в) 0.
Пример 4. Вычислить интеграл 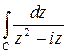 , если контур
, если контур 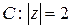 .
.
Решение. Подынтегральная функция 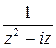 имеет две особые точки
имеет две особые точки 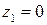 и
и 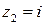 , причем обе они лежат внутри заданного контура
, причем обе они лежат внутри заданного контура  . Непосредственно формулу (6) применить нельзя.
. Непосредственно формулу (6) применить нельзя.
1 способ. Представим дробь 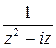 в виде суммы элементарных дробей и воспользуемся линейным свойством интеграла:
в виде суммы элементарных дробей и воспользуемся линейным свойством интеграла:
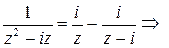
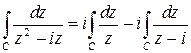
Плотность каждого из полученных интегралов Коши 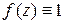 , ядро первого интеграла
, ядро первого интеграла 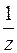 ,
, 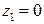 ; второго –
; второго – 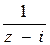 ,
, 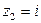 . Значит,
. Значит, 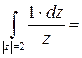
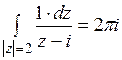 .
.
Тогда

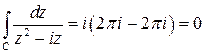 .
.
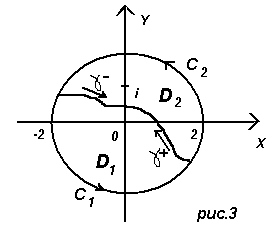
2 способ. Проведем произвольно линию 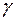 между точками
между точками 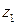 и
и 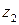 , разделяющую область
, разделяющую область 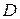 на части
на части 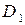 и
и 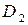 (рис.3) так, что
(рис.3) так, что 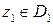 ,
, 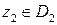 . При этом контур
. При этом контур  разбивается на части
разбивается на части 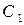 и
и 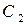 . Область
. Область 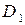 с границей
с границей 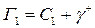 содержит внутри единственную особую точку
содержит внутри единственную особую точку 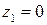 , значит,
, значит,
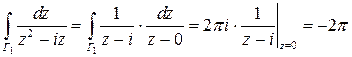 .
.
Область 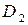 с границей
с границей 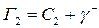 содержит единственную особую точку
содержит единственную особую точку 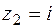 , значит,
, значит,
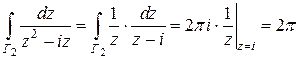 .
.
Складываем оба результата. С учетом аддитивности интеграла получаем
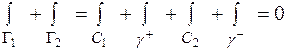 .
.
Но интегралы по 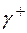 и по
и по 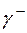 взаимно уничтожаются, поэтому
взаимно уничтожаются, поэтому
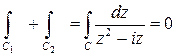 .?
.?
Задача 3. Вычислить интеграл 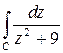 , если обе особые точки
, если обе особые точки 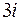 и
и 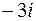 лежат внутри контура
лежат внутри контура  . Ответ: 0.
. Ответ: 0.
Если контур представляет собой окружность радиуса 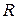 с центром в точке
с центром в точке  , (
, (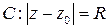 ), то замена
), то замена 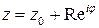 позволяет получить из формулы Коши теорему о среднем:
позволяет получить из формулы Коши теорему о среднем:
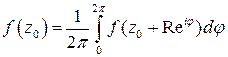 .
.
То есть значение аналитической функции в центре круга равно среднему арифметическому из ее значений на окружности этого круга.
Из аналитичности функции 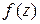 в точке
в точке 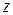 , то есть из существования ее первой производной в некоторой окрестности этой точки, и интегральной формулы Коши следует существование в окрестности той же точки производных любого порядка данной функции, причем
, то есть из существования ее первой производной в некоторой окрестности этой точки, и интегральной формулы Коши следует существование в окрестности той же точки производных любого порядка данной функции, причем
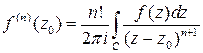 (7)
(7)
Пример 5. Вычислить интеграл 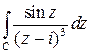 , если
, если  – замкнутый контур, обходящий точку
– замкнутый контур, обходящий точку 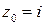 .
.
Решение. Положим в формуле (3) 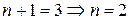 , тогда
, тогда
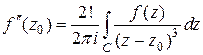 .
.
Сопоставляя с заданным интегралом, видим, что 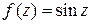 и
и 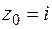 , т.е.
, т.е.
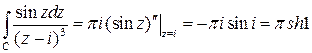 ?.
?.
Задача 4. Вычислить интеграл 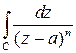
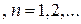 , если
, если  – замкнутый контур, содержащий внутри точку
– замкнутый контур, содержащий внутри точку 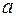 (воспользоваться формулой (7)). Сравнить результат с примером 2. Ответ:
(воспользоваться формулой (7)). Сравнить результат с примером 2. Ответ: 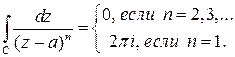
 2015-05-13
2015-05-13 30569
30569
