Если производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А.
Пусть производится n независимых одинаковых испытаний, в каждом из которых событие А может наступить с одной и той же вероятностью p. Тогда вероятность 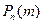 того, что событие наступило m раз в этой серии испытаний можно вычислить по одной из следующих формул: формула Бернулли, формула Пуассона, локальная теорема Муавра-Лапласа. Если число испытаний того, что событие наступило m раз в этой серии испытаний можно вычислить по одной из следующих формул: формула Бернулли, формула Пуассона, локальная теорема Муавра-Лапласа. Если число испытаний 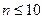 , то для вычисления вероятности применяют формулу Бернулли, если же , то для вычисления вероятности применяют формулу Бернулли, если же 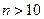 , то формулу Пуассона (если , то формулу Пуассона (если 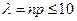 ) или локальную теорему Муавра-Лапласа (в остальных случаях). Формула Бернулли: ) или локальную теорему Муавра-Лапласа (в остальных случаях). Формула Бернулли: 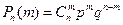 . (2.8) . (2.8) |
Вероятности того, что в n испытаниях событие наступит: а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз, находят соответственно по формулам:
а) 
б) 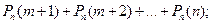
в) 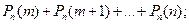
г) 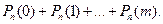
Пример 21. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна 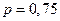 . Найдите вероятность того, что в ближайшие 6 суток расход электроэнергии в течение четырех суток не превысит нормы.
. Найдите вероятность того, что в ближайшие 6 суток расход электроэнергии в течение четырех суток не превысит нормы.
Решение. Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток постоянна и равна 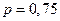 . Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна:
. Следовательно, вероятность перерасхода электроэнергии в каждые сутки также постоянна и равна: 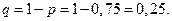
Искомая вероятность по формуле Бернулли равна:
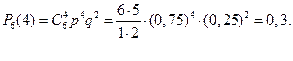
Пример 22. Монету бросают 6 раз. Найдите вероятность того, что герб выпадет: а) менее двух раз; б) не менее двух раз.
Решение. Вероятность появления герба в одном испытании равна: 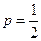 .
.
а) вероятность выпадения герба менее двух раз в шести независимых испытаниях равна:
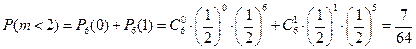 .
.
б) вероятность появления герба в шести независимых испытаниях не менее двух раз, находим по формуле:
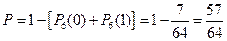 .
.
Пример 23. Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются)?
Решение. Играют равносильные шахматисты, поэтому вероятность выигрыша каждого равна: 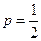 . Следовательно, вероятность проигрыша равна:
. Следовательно, вероятность проигрыша равна: 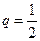 .
.
Так как во всех партиях вероятность выигрыша постоянна и безразлично, в какой последовательности будут выиграны партии, то применима формула Бернулли.
Вероятность того, что две партии из четырех будут выиграны:
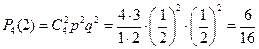 .
.
Вероятность того, что будут выиграны три партии из шести:
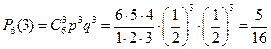 .
.
Так как то вероятнее выиграть две партии из четырех, чем три из шести 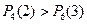 .
.
Формула Пуассона: если вероятность 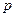 – постоянна и мала, число испытаний
– постоянна и мала, число испытаний 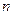 – велико и число
– велико и число 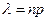 – незначительно (будем полагать
– незначительно (будем полагать 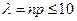 ) получается приближенная формула Пуассона:
) получается приближенная формула Пуассона:
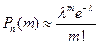 . (2.9)
. (2.9)
Пример 24. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равно 0,0002. Найдите вероятность того, что на базу прибудут 3 негодных изделия.
Решение. Имеем 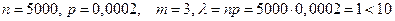
По формуле Пуассона искомая вероятность приближенно равна:
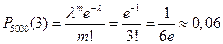 .
.
Пример 25. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найдите вероятность того, что магазин получит ровно две разбитых бутылки.
Решение. Число 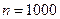 велико, вероятность
велико, вероятность 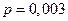 мала,
мала, 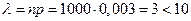 , поэтому можно использовать формулу Пуассона:
, поэтому можно использовать формулу Пуассона: 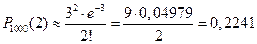 .
.
Локальная теорема Муавра-Лапласа: если вероятность 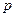 наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет
наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что событие А произойдет 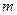 раз в
раз в 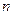 независимых испытаниях при достаточно большом числе
независимых испытаниях при достаточно большом числе 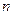 , приближенно равна:
, приближенно равна:
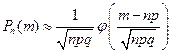 , где
, где 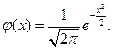 (2.10)
(2.10)
Значения функции 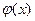 для
для 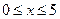 приводятся в специальной таблице. Эта функция обладает свойствами: 1)
приводятся в специальной таблице. Эта функция обладает свойствами: 1) 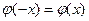 ; 2)
; 2) 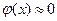
при 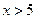 .
.
Пример 26. Найдите вероятность того, что событие А наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию, 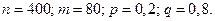 По локальной теореме Муавра-Лапласа получаем:
По локальной теореме Муавра-Лапласа получаем:
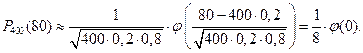
По таблице приложения находим 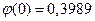 . Искомая вероятность
. Искомая вероятность
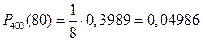 .
.
Вероятность того, что событие наступит в пределах от 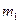 до
до 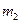 раз, можно вычислить, используя интегральную теорему Муавра-Лапласа.
раз, можно вычислить, используя интегральную теорему Муавра-Лапласа.
Интегральная теорема Муавра-Лапласа: если вероятность 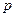 наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число
наступления события А в каждом испытании постоянна и отлична от 0 и 1, то вероятность того, что число 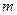 наступления события А в
наступления события А в 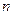 независимых испытаниях заключено в пределах от
независимых испытаниях заключено в пределах от 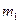 до
до 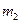 при достаточно большом числе
при достаточно большом числе 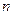 , приближенно равна:
, приближенно равна:
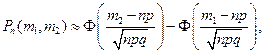
где 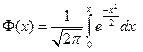 – функция Лапласа. (2.11)
– функция Лапласа. (2.11)
Значения функции 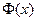 для
для 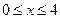 даны в специальной таблице. Эта функция обладает свойствами: 1)
даны в специальной таблице. Эта функция обладает свойствами: 1) 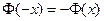 ; 2)
; 2) 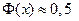 при
при 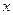 >4.
>4.
Пример 27. Вероятность того, что деталь не прошла проверку ОТК, равна 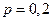 . Найдите вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
. Найдите вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение. По условию  Воспользуемся интегральной теоремой Муавра-Лапласа:
Воспользуемся интегральной теоремой Муавра-Лапласа:
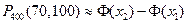 , где
, где 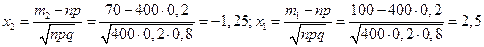 .
.
Таким образом, 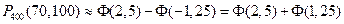 .
.
По таблице приложения: 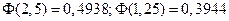 . Искомая вероятность
. Искомая вероятность 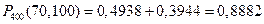 .
.
Число 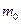 (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна
(наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна 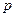 ) называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях
) называется наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях 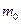 раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число 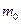 определяется из двойного неравенства:
определяется из двойного неравенства:
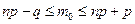 . (2.12)
. (2.12)
Пример 28. Товаровед осматривает 24 образца товаров. Вероятность того, что каждый из образцов будет признан годным к продаже, равна 0,6. Найдите наивероятнейшее число образцов, которые товаровед признает годными к продаже.
Решение. По условию, 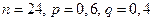 . Найдем наивероятнейшее число годных к продаже образцов товаров из двойного неравенства
. Найдем наивероятнейшее число годных к продаже образцов товаров из двойного неравенства 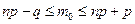 . Подставляя данные задачи, получим:
. Подставляя данные задачи, получим: 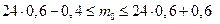 или
или 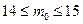 .
.
Наивероятнейших значений два: 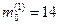 и
и 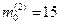 .
.
 2015-05-13
2015-05-13 6249
6249
