Функция 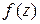 , однозначная и аналитическая в точке
, однозначная и аналитическая в точке  (регулярная в
(регулярная в  ), представляется в окрестности этой точки рядом Тейлора
), представляется в окрестности этой точки рядом Тейлора
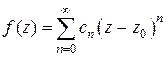 , (1)
, (1)
коэффициенты 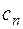 которого вычисляются по формулам
которого вычисляются по формулам
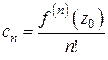 ,
, 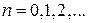 (2)
(2)
Круг сходимости ряда (1) имеет центр в точке  . Его граница проходит через ближайшую к
. Его граница проходит через ближайшую к  особую точку функции
особую точку функции 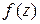 . Иначе: радиус сходимости ряда Тейлора равен расстоянию от центра
. Иначе: радиус сходимости ряда Тейлора равен расстоянию от центра  до ближайшей особой точки функции
до ближайшей особой точки функции 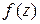 .
.
Имеет место единственность представления аналитической функции 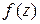 степенным рядом: всякий степенный ряд вида (1) является рядом Тейлора для своей суммы
степенным рядом: всякий степенный ряд вида (1) является рядом Тейлора для своей суммы 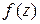 .
.
Пример 1. Найти первые три члена разложения функции 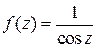 в ряд по степеням
в ряд по степеням 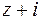 и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Решение. Коэффициенты 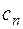 ряда
ряда 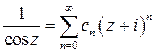 определяются по формулам (2), где
определяются по формулам (2), где 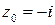 . Находим сначала производные:
. Находим сначала производные:
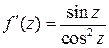 ,
, 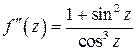 .
.
По формулам (2) находим тейлоровские коэффициенты:
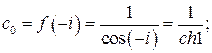
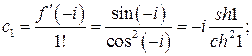
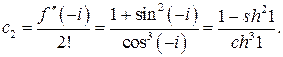
Значит, 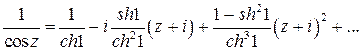
Особые точки функции 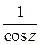 найдем из условия равенства нулю знаменателя:
найдем из условия равенства нулю знаменателя: 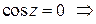
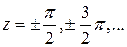 . Из полученных точек ближайшими к центру круга
. Из полученных точек ближайшими к центру круга 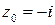 являются точки
являются точки 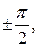 их расстояние от центра равно
их расстояние от центра равно 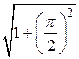 . Значит, радиус сходимости полученного ряда
. Значит, радиус сходимости полученного ряда 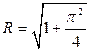 . ☻
. ☻
Задача 1. Найти несколько первых членов разложения функции 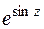 в ряд по степеням
в ряд по степеням 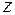 и определить радиус сходимости ряда.
и определить радиус сходимости ряда.
Ответ: 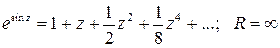 .
.
Пример 2. Разложить в ряд Тейлора функцию 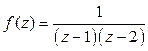 в окрестности точки
в окрестности точки 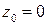 и найти радиус сходимости ряда.
и найти радиус сходимости ряда.
Решение. Представим данную функцию в виде суммы элементарных дробей:
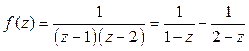 .
.
Первое слагаемое 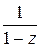 при
при 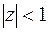 есть сумма членов бесконечной геометрической прогрессии (см. пр.1 §8):
есть сумма членов бесконечной геометрической прогрессии (см. пр.1 §8): 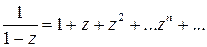 , этот ряд сходится в круге
, этот ряд сходится в круге 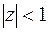 .
.
Второе слагаемое 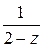 преобразуем так, чтобы опять можно было получить сумму геометрического ряда, то есть выделим множитель
преобразуем так, чтобы опять можно было получить сумму геометрического ряда, то есть выделим множитель 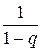 , где
, где 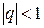 – знаменатель прогрессии:
– знаменатель прогрессии: 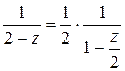 . При
. При 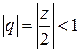 получаем сумму членов бесконечной геометрической прогрессии:
получаем сумму членов бесконечной геометрической прогрессии:
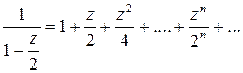
Этот ряд сходится в круге 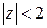 (в частности, он сходится в круге
(в частности, он сходится в круге 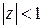 с меньшим радиусом).
с меньшим радиусом).
Осталось сложить полученные ряды:
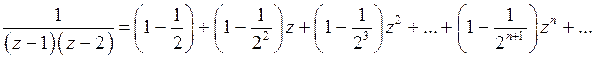
Ряд, стоящий справа, сходится в круге 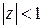 , то есть радиус сходимости
, то есть радиус сходимости 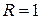 .
.
Можно было из условия 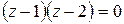 найти особые точки заданной функции:
найти особые точки заданной функции: 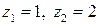 и вычислить радиус сходимости как расстояние ближайшей из них от точки
и вычислить радиус сходимости как расстояние ближайшей из них от точки 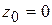 . Естественно, опять приходим к результату
. Естественно, опять приходим к результату 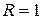 . ☻
. ☻
Задача 2. Показать, что функция 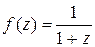 в окрестности точки
в окрестности точки 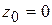 представляется рядом
представляется рядом
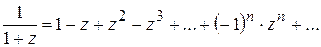 (*)
(*)
Задача 3. Разложить функцию 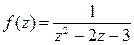 в ряд Тейлора по степеням
в ряд Тейлора по степеням 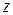 и найти радиус сходимости полученного ряда.
и найти радиус сходимости полученного ряда.
Ответ: 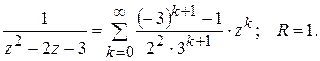
Пример 3. Разложить функцию 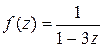 в ряд Тейлора в окрестности точки
в ряд Тейлора в окрестности точки 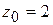 .
.
Решение. Требуется разложить данную функцию по степеням 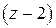 . Предварительно преобразуем функцию к виду
. Предварительно преобразуем функцию к виду 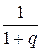 , выделяя разность
, выделяя разность 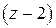 :
:
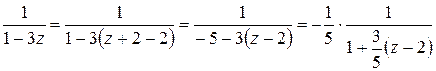 .
.
Заменяя в разложении (*) 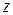 на
на 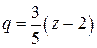 , получим
, получим
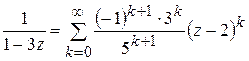 .
.
Это разложение имеет место при условии 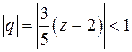 т.е.
т.е. 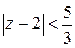 . Значит, радиус сходимости ряда
. Значит, радиус сходимости ряда 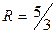 . Это же значение для
. Это же значение для 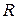 получим, определяя расстояние особой точки данной функции
получим, определяя расстояние особой точки данной функции 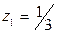 от центра
от центра 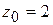 . ☻
. ☻
Полезно запомнить:
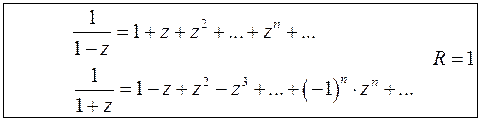
Задача 4. Используя бесконечную геометрическую прогрессию, разложить функцию 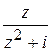 в ряд по степеням
в ряд по степеням 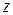 . Найти радиус сходимости полученного ряда.
. Найти радиус сходимости полученного ряда.
Ответ: 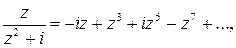
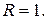
Пример 4. Разложить функцию 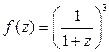 в ряд Тейлора,
в ряд Тейлора, 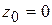 ..
..
Решение. Воспользуемся разложением функции 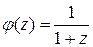 :
:
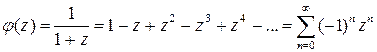 .
.
В круге 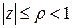 этот ряд сходится равномерно, поэтому его можно почленно дифференцировать. Находим последовательно
этот ряд сходится равномерно, поэтому его можно почленно дифференцировать. Находим последовательно
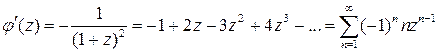
 2015-05-13
2015-05-13 6410
6410