Алгебраический критерий устойчивости

(КРИТЕРИЙ РАУСА-ГУРВИЦА)

Австрийские математики Раус и Гурвиц в 1895 году нашли условия, при которых многочлен любой степени не содержит корней с положительной вещественной частью.

Рассмотрим характеристическое уравнение САУ n -го порядка:

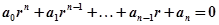
Алгебраический критерий устойчивости (критерий Рауса-Гурвица) формулируется следующим образом:

Для устойчивости САУ необходимо и достаточно, чтобы при 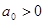все диагональные миноры квадратной матрицы Гурвица, составленной из коэффициентов характеристического уравнения, были положительны.

Определитель Гурвица составляется из коэффициентов характеристического уравнения следующим образом:

- по диагонали определителя выписываются все коэффициенты от a₁ до a_n в порядке возрастания (слева – направо, сверху – вниз);

- заполнение столбцов от диагонального коэффициента производится: вверх - коэффициентами уравнения с большими индексами, а вниз - коэффициентами уравнения с меньшими индексами. Места коэффициентов с отрицательными индексами и индексами больше " n " заполняются нулями:

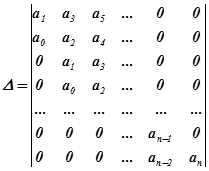
Из этого критерия вытекают следствия:

1) для устойчивости системы, описываемой уравнениями до 2-го порядка включительно, необходимо и достаточно, чтобы коэффициенты характеристического уравнения были больше нуля;

2) для системы 3-го порядка

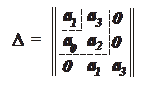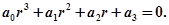
Матрица Гурвица в этом случае запишется следующим образом:

Условия устойчивости:

;

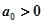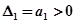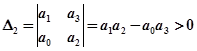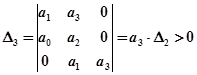Третий (последний) определитель 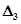дает условие .

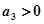Таким образом, для уравнения третьего порядка уже недостаточно положительности всех коэффициентов характеристического уравнения.

3) Для системы 4-го порядка 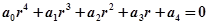необходимые и достаточные условия устойчивости помимо указанных для системы третьего порядка записываются в виде неравенства .

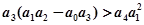Рассмотрим примеры.

Пример 1. Определить устойчивость системы с передаточной функцией:

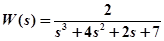Рассмотрим характеристическое уравнение:

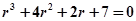Матрица Гурвица записывается следующим образом:

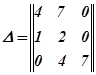
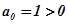
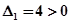
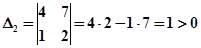
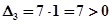Все диагональные миноры больше нуля, следовательно, система устойчива.

Пример 2. Определить устойчивость системы с передаточной функцией:

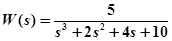Рассмотрим характеристическое уравнение:

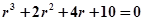Матрица Гурвица записывается следующим образом:

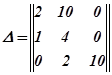
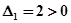
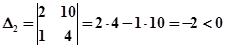
Один из диагональных миноров меньше нуля, следовательно, система неустойчива.

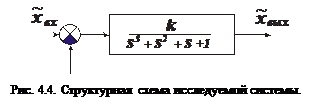Пример 3. Определить значения k, при которых система (рис. 4.4) будет устойчива.

Передаточная функция системы определится выражением:

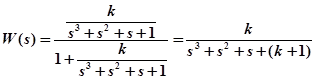Рассмотрим характеристическое уравнение:

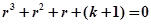Матрица Гурвица записывается следующим образом:

;

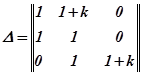
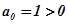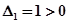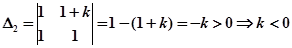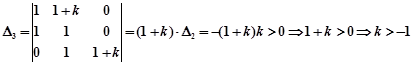Таким образом, система будет устойчива при значениях k из диапазона (-1;0).

Алгебраический критерий устойчивости используется для анализа систем не выше 5-го порядка. Для систем, порядок которых больше пяти, могут быть использованы специальные таблицы Рауса, составленные из коэффициентов 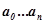и их комбинаций. Но это трудоёмкая операция. Кроме того, критерий Рауса-Гурвица при n>5 лишен возможности внутренней (промежуточной) проверки и имеет большую вероятность погрешности из-за многочисленных арифметических действий.