Частотный критерий устойчивости Найквиста

Иногда в практике возникает необходимость в анализе устойчивости замкнутой САУ по характеристикам разомкнутой её части. Критерий Найквиста позволяет определить устойчивость замкнутой системы по виду АФЧХ разомкнутой системы (АФЧХ 2-го рода).

;

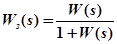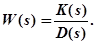
Для доказательства критерия Найквиста введём вспомогательную передаточную функцию

,

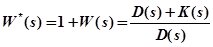W(s) - передаточная функция системы в разомкнутом состоянии;

D_з(s)=D(s)+K(s) - собственный оператор замкнутой системы;

D(s) - собственный оператор системы в разомкнутом состоянии.

Как правило, порядок оператора возмущения K(s) меньше порядка собственного оператора D(s), поэтому порядки собственного оператора замкнутой системы и системы в разомкнутом состоянии совпадают.

Переходя в частотную область (s=j 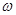), получим:

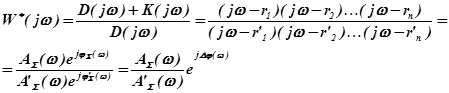
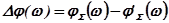
r₁, r₂,…r_n - корни уравнения D_з(r)=0,

r'₁, r'₂,…r'_n - корни уравнения D(r)=0.

При анализе устойчивости замкнутой системы могут быть 2 случая:

- разомкнутая система устойчива,

- разомкнутая система неустойчива.

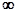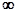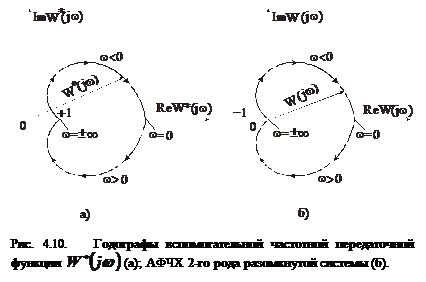
Рассмотрим случай, когда разомкнутая система устойчива. Будем изменять частоту от - до + и изобразим получившуюся амплитудно-фазовую частотную характеристику 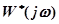на комплексной плоскости (рис. 4.10,а). Рассмотрим результирующий угол поворота вектора 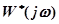при изменении частоты от - 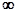до + 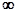. Этот угол представляет собой изменение .

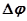Числитель в выражении

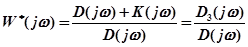(4.6)

представляет собой характеристический комплекс замкнутой системы. Для того чтобы система была устойчивой в замкнутом состоянии необходимо изменение аргумента 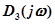в диапазоне частот 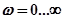равно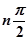е , где 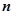- степень характеристического полинома. При изменении частоты от - 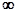до + 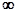аргумент 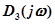изменится на величину .

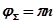Знаменатель в выражении (4.6) представляет собой характеристический комплекс разомкнутой системы той же степени n. Так как мы рассматриваем случай устойчивой разомкнутой системы, то результирующий угол поворота вектора 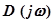при изменении частоты от - 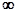до + 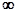будет равен .

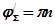Отсюда следует, что в рассмотренном случае результирующий угол поворота вектора 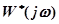будет равен нулю: 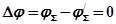. Это означает, что для устойчивой в замкнутом состоянии системы годограф вектора 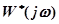не должен охватывать начала координат (рис. 4.10,а).

Частотная функция 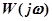разомкнутой системы отличается от вспомогательной функции 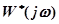на единицу. Поэтому можно строить амплитудно-фазовую частотную характеристику разомкнутой системы и по ее виду анализировать устойчивость замкнутой САУ. В этом случае амплитудно-фазовая частотная характеристика разомкнутой системы не должна охватывать точку с координатами (-1; j0) (рис. 4.10,б).

Из доказанного следует формулировка критерия Найквиста:

Для устойчивости замкнутой САУ, полученной замыканием устойчивой разомкнутой системы, необходимо и достаточно, чтобы АФЧХ разомкнутой системы не охватывала точку с координатами (-1; j0).

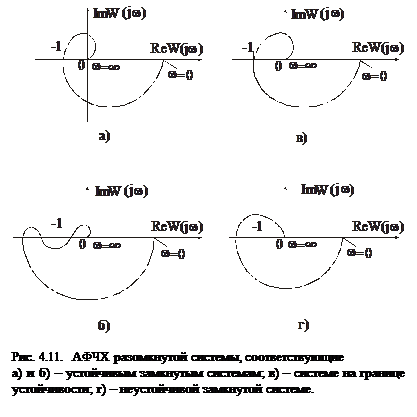
На рис. 4.11 приведены примеры частотных характеристик разомкнутых систем, соответствующих устойчивым и неустойчивым замкнутым системам.

Вследствие симметрии ветвей (относительно действительной оси) обычно строят только ветви АФЧХ, соответствующие положительному диапазону частот.

Второй случай - разомкнутая система неустойчива.

Наличие неустойчивости системы в разомкнутом состоянии не означает, что система будет неустойчивой в замкнутом состоянии. Она может быть как устойчивой, так и неустойчивой. Однако формулировка критерия устойчивости Найквиста при этом несколько меняется. Пусть знаменатель передаточной функции разомкнутой системы 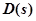степени n содержит k корней с положительной вещественной частью.

Тогда при изменении частоты от - 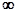до + 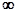аргумент D(j 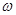) повернётся на угол .

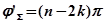Для устойчивой замкнутой системы при изменении частоты от - 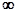до + 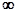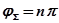. Следовательно, аргумент 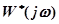будет равен

.

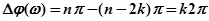Это означает, что вектор годографа 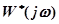охватывает на комплексной плоскости начало координат в положительном направлении столько раз, сколько корней характеристического уравнения системы в разомкнутом состоянии находится в правой полуплоскости.

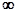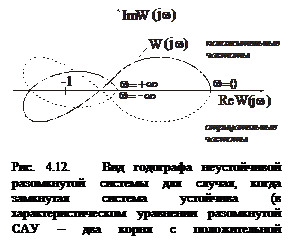
Итак, для устойчивости замкнутой системы, полученной замыканием неустойчивой разомкнутой системы, необходимо и достаточно, чтобы при изменении частоты от - до + 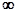АФЧХ разомкнутой системы охватывала в положительном направлении точку с координатами (-1;j0) столько раз, сколько положительных корней имеется в характеристическом уравнении, соответствующем разомкнутой системы (рис. 4.12). При изменении 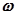от 0 до + 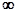годограф АФЧХ 2-го рода должен охватывать точку (-1;j0) 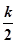раз.

Таким образом, при использовании критерия Найквиста, вообще говоря, необходимо убедиться в том, имеются ли в знаменателе передаточной функции разомкнутой системы корни, лежащие в правой полуплоскости (корни с положительной вещественной частью), и сколько имеется таких корней.

Следует заметить, что в практике желательно избегать второго случая, т.е. необходимо использовать только устойчивые в разомкнутом состоянии системы.

Это объясняется тем, что, если система в разомкнутом состоянии неустойчива, то при её замыкании и имеющихся в реальной системе нелинейностях может на некоторых режимах произойти нарушение устойчивой работы и возникновение автоколебаний.

Для решения многих инженерных задач обеспечения устойчивости используют частный случай критерия Найквиста.