Критерий устойчивости Михайлова

Рассмотрим САУ, описываемую передаточной функцией

.

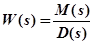При исследовании устойчивости по частотному критерию Михайлова анализируется собственный оператор системы

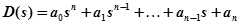
в котором производится замена .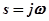

Сгруппировав действительные и мнимые члены, получим так называемую амплитудно-фазовую частотную характеристику 1-го рода.

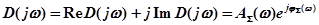
Если построить график функции 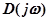на комплексной плоскости, то получаем годограф АФЧХ 1-го рода (годограф Михайлова).

По расположению годографа Михайлова относительно оси координат судят об устойчивости САУ. Рассмотрим доказательство критерия Михайлова.

Представим D(s) в виде произведения сомножителей

,

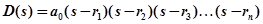где 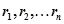- корни характеристического уравнения.

Когда переходим от s к 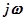, получим характеристический комплекс:

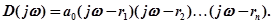(4.4)

Свойство: при перемножении комплексных чисел, представленных на комплексной плоскости в виде векторов, модули их перемножаются, а углы - складываются.

Каждый из сомножителей выражения (4.4) представляет собой комплексное число. Следовательно, 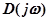представляет собой произведение n комплексных чисел. Поэтому результирующий угол поворота вектора 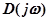на комплексной плоскости при изменении 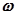от нуля до бесконечности будет равен сумме углов поворота отдельных сомножителей (4.4):

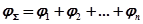(4.5)

Определим каждое слагаемое (4.5) в отдельности.

1. Пусть какой-либо корень, например 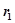, является вещественным и отрицательным, т. 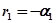е. , где 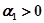. Сомножитель в выражении (4.4), определяемый этим корнем, будет тогда иметь вид .

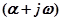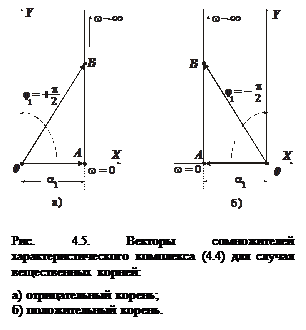Построим годограф этого вектора на комплексной плоскости при изменении w от нуля до бесконечности (рис. 4.5,а). При w=0 вещественная часть 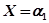, а мнимая 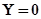. Этому соответствует точка А, лежащая на вещественной оси. При 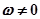вектор будет изменяться так, что его вещественная часть будет по-прежнему равна 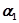, а мнимая часть 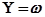(точка В на рис. 4.5,а). При увеличении частоты до бесконечности конец вектора уходит в бесконечность, при этом всегда оставаясь на вертикальной прямой, проходящей через точку А. Сам вектор поворачивается против часовой стрелки. Результирующий угол поворота вектора .

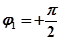2. Пусть теперь корень 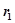является вещественным и положительным, т. е. 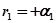, причем 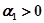. Тогда сомножитель в (4.4), определяемый этим корнем, будет иметь вид 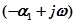. Построения, аналогичные проведенным в п. 1 показывают, что результирующий угол поворота будет 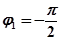. Знак минус говорит о том, что вектор поворачивается по часовой стрелке (рис. 4.5,б).

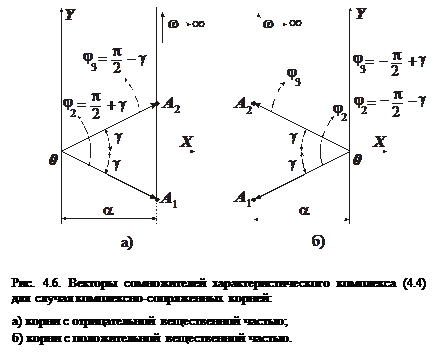3. Пусть два корня, например 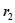и 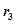представляют собой комплексные сопряжённые величины с отрицательной вещественной частью, т. е. 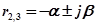. Сомножители в выражении (4.4), определяемые этими корнями, будут иметь вид .

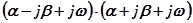При 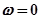начальные положения двух векторов определяются точкам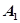и и 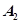(рис. 4.6,а). Один вектор повёрнут относительно вещественной оси по часовой стрелке на угол 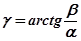, а второй вектор – на тот же угол против часовой стрелки. При увеличении от нуля до бесконечности концы обоих векторов уходят вверх в бесконечность и в пределе угол каждого вектора стремится к .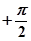

Результирующий угол поворота первого вектора 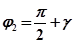. Результирующий угол поворота второго вектора 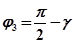. Вектор, соответствующий произведению 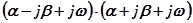повернется на угол .

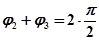4. Пусть те же комплексные корни имеют положительную вещественную часть, т. е. 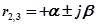. Построения, аналогичные проведенным в п. 3 показывают, что результирующий угол поворота вектора, соответствующего произведению двух сомножителей, будет 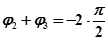(рис. 4.6 б).

Таким образом, если характеристическое уравнение будет иметь l корней с положительной вещественной частью, то каковы бы ни были эти корни (вещественные или комплексные), им будет соответствовать сумма углов поворотов, равная 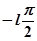. Всем же остальным 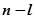корням характеристического уравнения, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворотов, равная 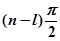. В результате общий угол поворота вектора 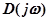при изменении w от нуля до бесконечности, согласно формуле (4.5), будет:

.

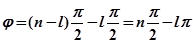С учетом этого критерий Михайлова можно сформулировать следующим образом:

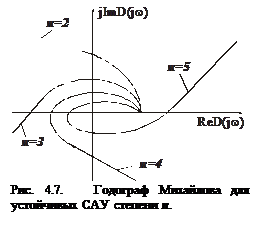
Для того чтобы САУ была устойчивой, необходимо и достаточно, чтобы годограф АФЧХ 1-го рода при изменении частоты 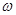от 0 до 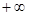последовательно проходил столько квадрантов, каков порядок характеристического уравнения (рис. 4.7).

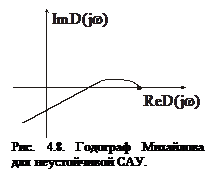В неустойчивых системах нарушается последовательность прохождения годографом Михайлова квадрантов, вследствие чего угол поворота вектора 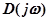оказывается меньшим чем 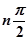(рис. 4.8).

Критерий Михайлова применяется для анализа устойчивости как замкнутых, так и разомкнутых систем. При исследовании устойчивости замкнутой САУ рассматривается собственный оператор замкнутой системы:

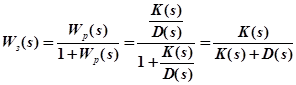
Собственный оператор замкнутой системы .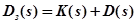

Пример. С использованием частотного критерия Михайлова определить устойчивость САУ, описываемой передаточной функцией

.

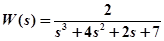В собственном операторе системы 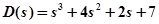производим замену :

;

.

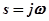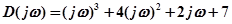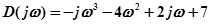Выделяем вещественную и мнимую части АФЧХ 1-го рода:

;

.

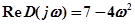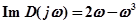Рассчитываем значения вещественной и мнимой части АФЧХ 1-го рода для нескольких различных значений частот:

w		0,2	0,3	1,32	1,41
ReD(jw)		6,84	6,64		-1	-9	-29
ImD(jw)		0,392	0,573	0,33		-4	-21

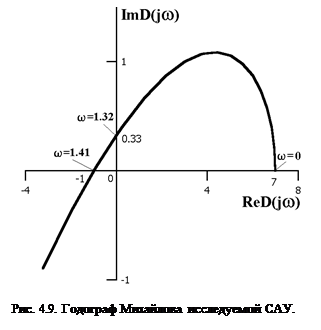По рассчитанным значениям строим годограф Михайлова (рис. 4.9). Годограф Михайлова последовательно охватывает 3 квадранта, следовательно, САУ устойчива.