2015-05-13
1828
Передаточная функция разомкнутой системы в этом случае:
, 
,
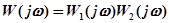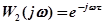где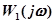 
- передаточная функция, соответствующая системе без запаздывания;
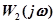- передаточная функция запаздывающего звена;
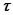- время запаздывания (
).
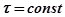По формуле Эйлера:
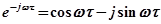- уравнение окружности с радиусом R=1.
Частотную функцию, соответствующую системе без запаздывания, можно представить в виде:
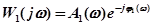. (4.7)
Модуль частотной функции запаздывающего звена равен единице, а ее аргумент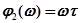 
. Представим выражение для 
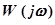в виде:
.
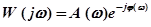Тогда модуль результирующей частотной передаточной функции:
,
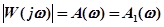а фаза
.
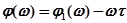Таким образом, наличие звена с запаздыванием не меняет модуля и вносит дополнительный фазовый сдвиг.
На рис. 4.13 изображена амплитудно-фазовая характеристика, соответствующая (4.7). Сплошной линией показана исходная характеристика при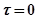 
, а пунктиром - характеристика, которая получается при наличии постоянного запаздывания 
.
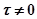Из этих характеристик видно, что наличие дополнительного фазового сдвига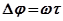 
“закручивает” годограф, особенно в высокочастотной области. Это, вообще говоря, ухудшает условия устойчивости, так как вся кривая приближается к точке (-1;j0).
По имеющемуся годографу 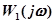можно определить критическое значение времени запаздывания 
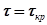, при котором система оказывается на границе устойчивости.
Для этой цели на годографе 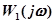отыскивается точка, для которой модуль равен единице (рис. 4.13). Частоту, соответствующую этой точке, обозначим 
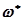, а фазу - 
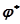. При введении постоянного запаздывания 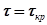условие совпадения этой точки с точкой (-1;j0) запишется следующим образом:
,
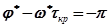откуда критическое значение запаздывания
.
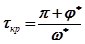Чтобы система, включающая звено чистого запаздывания, была устойчива, необходимо и достаточно, чтобы была устойчива система без учета запаздывания и время запаздывания было меньше критического.
Если имеется несколько точек пересечения АФЧХ с единичной окружностью, то получается ряд значений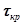 
. В этом случае необходимо время запаздывания в системе сравнить с наименьшим критическим.
