Структурно-устойчивой называется система, для которой без изменения числа элементов и порядка уравнения движения можно добиться устойчивости лишь изменением численных значений коэффициентов в уравнении движения.
Структурно-неустойчивой называется система, устойчивости которой нельзя добиться никакими изменениями коэффициентов в характеристическом уравнении движения.
В ряде случаев по виду структурной схемы можно решить, является система структурно-устойчивой или структурно-неустойчивой.
До сих пор рассматривались лишь устойчивые звенья и звенья, находящиеся на границе устойчивости (интегрирующие звенья с передаточной функцией 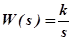 ). Принципиально возможно появление в системе и неустойчивых звеньев. Действительно, разомкнутая САУ может быть неустойчивой, что, однако, не исключает возможности стабилизации замкнутой системы. Если разомкнутая система неустойчива, то её характеристическое уравнение имеет корни, находящиеся в правой полуплоскости, т.е. знаменатель оператора разомкнутой системы содержит множители типа (1-sТ), где Т>0. В связи с указанным назовём звено с оператором
). Принципиально возможно появление в системе и неустойчивых звеньев. Действительно, разомкнутая САУ может быть неустойчивой, что, однако, не исключает возможности стабилизации замкнутой системы. Если разомкнутая система неустойчива, то её характеристическое уравнение имеет корни, находящиеся в правой полуплоскости, т.е. знаменатель оператора разомкнутой системы содержит множители типа (1-sТ), где Т>0. В связи с указанным назовём звено с оператором
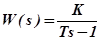
неустойчивым инерционным звеном.
 2015-05-13
2015-05-13 533
533








