2015-05-13
1871
(диаграмма Вышнеградского)
D-разбиение в плоскости двух параметров дает более полное представление о влиянии физических параметров САУ на устойчивость (рис. 4.24). Задачу построения D-разбиения в плоскости двух параметров для системы третьего порядка решил Вышнеградский И. А.
Случай системы 3-го порядка - наиболее часто встречается в САУ, когда объект регулирования описывается апериодическим звеном, а регулятор - колебательным (рис. 1.18).
Запишем собственный оператор системы в общем виде
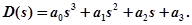
Для сведения этой задачи к вариации 2-х безразмерных коэффициентов и решения в общем виде проводим операцию нормализации и вместо s вводим другой аргумент:
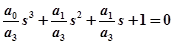; (4.10)
.
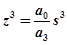Из последнего уравнения выразим оператор s через аргумент z:
;
.
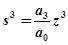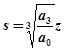С учётом этого выражения (4.10) можно переписать в виде:
;
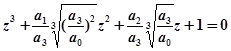или
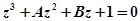, (4.11)
где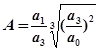 
;
.
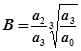В (4.11) делаем подставку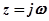 
и разбиваем полученный многочлен на действительную и мнимую части:
.
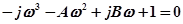Действительная часть:
.
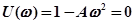Мнимая часть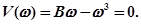 
Из полученных уравнений находим
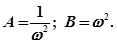(4.12)
Находим уравнение границы колебательной устойчивости:
|
|
|
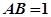- уравнение равнобокой гиперболы. Область устойчивости системы лежит выше этой кривой.
Составим матрицу Гурвица для рассматриваемой системы при значениях A и В, определяемых из (4.12):
.
.
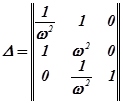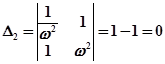Последний определитель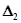 
доказывает, что кривая, определяемая выражением АВ=1, является границей колебательной устойчивости.
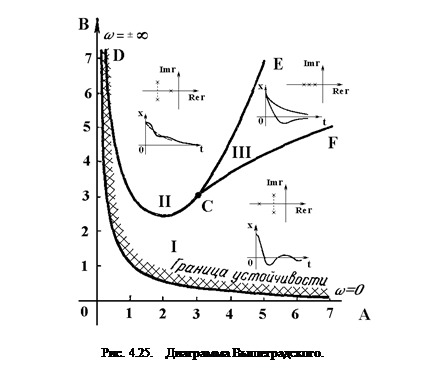
График на рис. 4.25 называется диаграммой Вышнеградского. Диаграмма Вышнеградского позволяет определить не только устойчивость САУ, но и вид переходного процесса в ней. Область устойчивости, в свою очередь, разбивается на 3 подобласти: I, II, III (рис. 4.25), соответствующие различному расположению корней характеристического уравнения. Отметим, что в точке С, где А=3 и В=3, характеристическое уравнение (4.11) принимает вид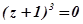 
. Следовательно, в этой точке все три корня равны: 
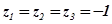. При этом для исходного характеристического уравнения (4.10) получаем 
.
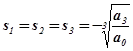В общем случае возможны два варианта:
1) все три корня вещественные;
2) один корень вещественный и два комплексных.
Границы между этими случаями определяются уравнениями (см. рис. 4.25):
кривая СD: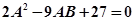 
; 
;
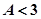кривые СЕ и СF: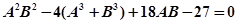 
; 
.
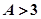В области III, где все корни вещественные, получим апериодический переходный процесс. Область III носит название области апериодических процессов. В области I быстрее затухает экспонента и переходный процесс в основном будет определяться колебательной составляющей. Это – область колебательных процессов. В области II, наоборот, быстрее затухает колебательная составляющая. Это будет область монотонных процессов.
