(МЕТОД D-РАЗБИЕНИЯ)
При проектировании систем необходимо знать области изменения того или иного параметра внутри которых САУ будет устойчива. Такие области называются областями устойчивости и получают их с помощью D-разбиения в плоскости искомого параметра, т.е. того параметра, относительно значений которого оценивается устойчивость системы.
В зависимости от того, сколько параметров системы меняется одновременно, решение ищется на прямой (один), на плоскости (два), на поверхности (три).
Для построения D-разбиения в плоскости одного параметра необходимо в собственном операторе системы 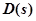 в явном виде выделить искомый параметр. Рассмотрим собственный оператор, который записывается в виде:
в явном виде выделить искомый параметр. Рассмотрим собственный оператор, который записывается в виде:
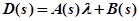 ,
,
где 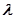 - искомый варьируемый параметр. Выделяя в уравнении
- искомый варьируемый параметр. Выделяя в уравнении 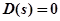 параметр
параметр 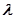 в явном виде, можно записать:
в явном виде, можно записать:
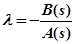 . (4.8)
. (4.8)
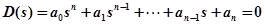 (4.9)
(4.9)
Коэффициенты 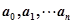 зависят от параметров САУ
зависят от параметров САУ 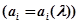 , следовательно корни характеристического уравнения всецело зависят от параметров системы и определяют ее устойчивость. При фиксированном значении параметров системы корни характеристического полинома (4.9) определенным образом располагаются на комплексной плоскости корней. Причем расположение всех корней в левой полуплоскости соответствует устойчивой системе. Расположение хотя бы одного корня в правой полуплоскости соответствует неустойчивой системе.
, следовательно корни характеристического уравнения всецело зависят от параметров системы и определяют ее устойчивость. При фиксированном значении параметров системы корни характеристического полинома (4.9) определенным образом располагаются на комплексной плоскости корней. Причем расположение всех корней в левой полуплоскости соответствует устойчивой системе. Расположение хотя бы одного корня в правой полуплоскости соответствует неустойчивой системе.
Пусть в общем случае корни характеристического уравнения (4.9) произвольно располагаются на комплексной плоскости. Предположим, что изменился режим работы системы, выразившийся в изменении параметра 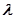 , который входит в один или несколько коэффициентов уравнения (4.9).
, который входит в один или несколько коэффициентов уравнения (4.9).
При непрерывном изменении 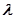 корни уравнения будут изменяться также непрерывно, т.е. будут менять свое положение на комплексной плоскости. При этом число корней остается постоянным и равным n. Очевидно, что существует такие области изменения параметра
корни уравнения будут изменяться также непрерывно, т.е. будут менять свое положение на комплексной плоскости. При этом число корней остается постоянным и равным n. Очевидно, что существует такие области изменения параметра 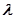 , в пределах которых число корней в левой и правой полуплоскостях не изменяется. Переход из одной области изменения
, в пределах которых число корней в левой и правой полуплоскостях не изменяется. Переход из одной области изменения 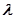 в другую соответствует переходу одного или нескольких корней из одной полуплоскости в другую (например, из левой в правую).
в другую соответствует переходу одного или нескольких корней из одной полуплоскости в другую (например, из левой в правую).
Границы, разделяющие области изменения параметра 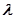 , при которых сохраняется постоянное число корней в левой и правой полуплоскостях, называются границами D–разбиения по параметру
, при которых сохраняется постоянное число корней в левой и правой полуплоскостях, называются границами D–разбиения по параметру 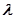 .
.
Значениям 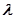 , лежащим на границе D–разбиения, соответствует один или несколько чисто мнимых корней характеристического уравнения.
, лежащим на границе D–разбиения, соответствует один или несколько чисто мнимых корней характеристического уравнения.
Из (4.8) при 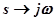 находим:
находим:
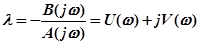 .
.
Изменяя значения 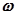 от
от 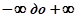 , построим в плоскости
, построим в плоскости 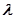 (или
(или 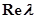 ,
, 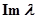 ) кривую, отображающую мнимую ось
) кривую, отображающую мнимую ось 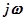 плоскости корней характеристического уравнения в плоскости
плоскости корней характеристического уравнения в плоскости 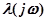 . Полученная кривая является кривой D–разбиения. Кривая D–разбиения для отрицательных и положительных частот симметрична относительно действительной оси, поэтому можно строить лишь ее участок, соответствующий изменению частот
. Полученная кривая является кривой D–разбиения. Кривая D–разбиения для отрицательных и положительных частот симметрична относительно действительной оси, поэтому можно строить лишь ее участок, соответствующий изменению частот 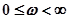 , и дополнить кривую зеркальным отображением относительно действительной оси. На рис. 4.20 построены плоскость корней характеристического уравнения (рис. 4.20,а) и кривая D–разбиения (рис. 4.20,б).
, и дополнить кривую зеркальным отображением относительно действительной оси. На рис. 4.20 построены плоскость корней характеристического уравнения (рис. 4.20,а) и кривая D–разбиения (рис. 4.20,б).
Построение кривой D–разбиения еще не решает вопроса о выделении области устойчивости. Последняя должна представлять собой совокупность точек плоскости, в которых все корни характеристического уравнения замкнутой системы имеют отрицательные вещественные части. В то же время кривая D–разбиения представляет собой только совокупность точек, в которых характеристическое уравнение имеет, по крайней мере, хотя бы один чисто мнимый корень 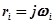 . Для того, чтобы решить вопрос о выделении области устойчивости, необходимо по определенным правилам заштриховать кривую D–разбиения.
. Для того, чтобы решить вопрос о выделении области устойчивости, необходимо по определенным правилам заштриховать кривую D–разбиения.
При перемещении в плоскости корней характеристического уравнения вдоль мнимой оси от 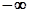 до
до 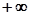 (рис. 4.20,а), область, в которой корни имеют отрицательные вещественные части, будет находиться все время слева. Заштрихуем мнимую ось плоскости корней характеристического уравнения слева. Имея это в виду, будем теперь перемещаться вдоль кривой D-разбиения от точки
(рис. 4.20,а), область, в которой корни имеют отрицательные вещественные части, будет находиться все время слева. Заштрихуем мнимую ось плоскости корней характеристического уравнения слева. Имея это в виду, будем теперь перемещаться вдоль кривой D-разбиения от точки 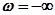 к точке, соответствующей
к точке, соответствующей 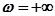 . Выполним штриховку этой кривой тоже слева (рис. 4.20,б). Таким образом, получим четыре зоны I, II, III, IV.
. Выполним штриховку этой кривой тоже слева (рис. 4.20,б). Таким образом, получим четыре зоны I, II, III, IV.
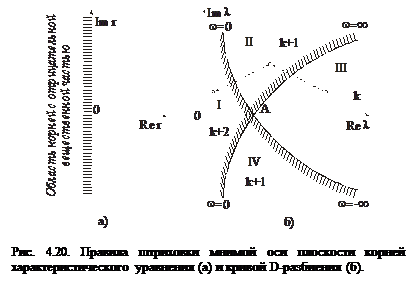 |
Допустим, что каким-либо способом удалось установить, что в зоне III имеется k отрицательных корней слева от мнимой оси. Если при переходе в другую зону кривая D-разбиения пересекаются с незаштрихованной стороной на заштрихованную, то этой зоне соответствует полином с
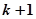 корнем в левой полуплоскости корней характеристического уравнения (рис. 4.20,б). При переходе через кривую с заштрихованной стороны на незаштрихованную число отрицательных корней уменьшается на единицу. Если штриховка двойная (что соответствует точке пересечения кривых D-разбиения - точке А на рис. 4.20,б), то число корней увеличится на 2, т. е. в этой зоне имеем
корнем в левой полуплоскости корней характеристического уравнения (рис. 4.20,б). При переходе через кривую с заштрихованной стороны на незаштрихованную число отрицательных корней уменьшается на единицу. Если штриховка двойная (что соответствует точке пересечения кривых D-разбиения - точке А на рис. 4.20,б), то число корней увеличится на 2, т. е. в этой зоне имеем 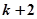 отрицательных корня.
отрицательных корня. Практически представляет интерес рассмотрение только действительных значений параметра 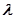 . Поэтому, построив кривые D-разбиения и определив число корней в каждой зоне, необходимо найти тот отрезок действительной оси на плоскости
. Поэтому, построив кривые D-разбиения и определив число корней в каждой зоне, необходимо найти тот отрезок действительной оси на плоскости 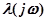 , который принадлежит области устойчивости. Из предлагаемой области устойчивости выбирается значение параметра
, который принадлежит области устойчивости. Из предлагаемой области устойчивости выбирается значение параметра 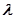 (как правило, на действительной оси, т. к.
(как правило, на действительной оси, т. к. 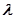 - действительное число - жёсткость, масса, коэффициент трения и т. п.), которое подставляется в характеристическое уравнение. Затем, воспользовавшись одним из критериев устойчивости, определяется устойчивость САУ при выбранном значении
- действительное число - жёсткость, масса, коэффициент трения и т. п.), которое подставляется в характеристическое уравнение. Затем, воспользовавшись одним из критериев устойчивости, определяется устойчивость САУ при выбранном значении 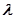 . Если система будет устойчива с этим значением
. Если система будет устойчива с этим значением 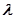 , то она будет устойчива во всей области, из которой выбрано значение
, то она будет устойчива во всей области, из которой выбрано значение 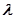 .
.
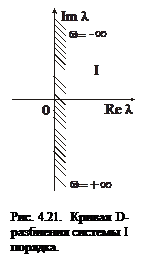 Пример.
Пример.
Уравнение 1-го порядка
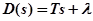 ,
,
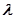 - варьируемый параметр. Приравниваем собственный оператор
- варьируемый параметр. Приравниваем собственный оператор 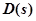 к нулю:
к нулю:
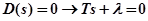 .
.
Из последнего уравнения выражаем 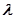 в явном виде.
в явном виде.
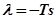 ,
, 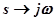 .
.
Получаем выражение для построения кривой D-разбиения.
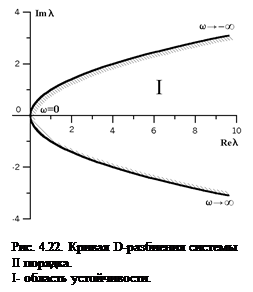
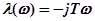 (рис. 4.21).
(рис. 4.21).
I- область устойчивости.
 Пример.
Пример.
Система 2-го порядка
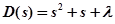
Приравниваемый собственный оператор 
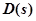 к нулю:
к нулю:
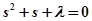 .
.
Из последнего уравнения выражаем 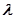 в явном виде:
в явном виде:
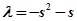 ,
, 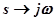 .
.
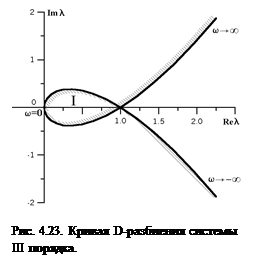
Получаем выражение для построения кривой D-разбиения (рис. 4.22):
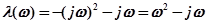 .
.
 Пример.
Пример.
Система 3-го порядка:
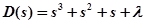 .
.
Приравняем собственный оператор 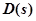 к нулю:
к нулю:
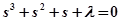 .
.
Из последнего уравнения выражаем 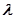 в явном виде:
в явном виде:
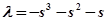 ;
; 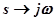
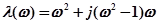 На рис. 4.23 изображена кривая D-разбиения.
На рис. 4.23 изображена кривая D-разбиения.
Область I обладает наибольшим числом корней с отрицательной вещественной частью. Поэтому выбираем из этой области 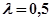 и проверяем на устойчивость с использованием, например, критерия Гурвица.
и проверяем на устойчивость с использованием, например, критерия Гурвица.
Характеристическое уравнение в этом случае запишется в виде:
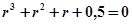 .
.
Матрица Гурвица для данного уравнения:
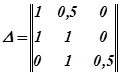 .
.
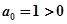 ;
;
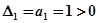 ;
;
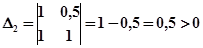 .
.
Итак система устойчива при 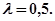 Следовательно, она будет устойчива во всей области I изменения параметра
Следовательно, она будет устойчива во всей области I изменения параметра 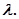
 2015-05-13
2015-05-13 1056
1056
