Теорема Айзермана М.А

Для того, чтобы замкнутая система была структурно- устойчивой необходимо и достаточно, чтобы выполнялись неравенства

r+q<2,

n>4m,

где r - число интегрирующих звеньев,

q - число неустойчивых инерционных звеньев,

m - число консервативных звеньев (),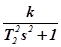

n - порядок собственного оператора системы.

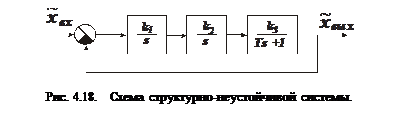
Рассмотрим пример системы, изображенной на рис. 4.18. В этом случае

;

;

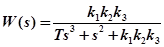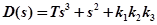Применим критерий Гурвица .

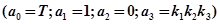Матрица Гурвица для рассматриваемого случая запишется следующим образом:

;

;

;

.

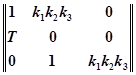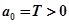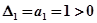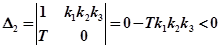Отсюда видно, что для такой структуры никаким изменением коэффициентов обеспечить устойчивость системы невозможно.

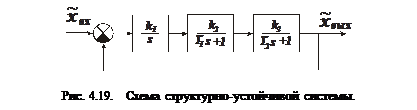
Заменим одно из интегрирующих звеньев на апериодическое (рис. 4.19). В этом случае передаточная функция системы запишется в виде:

.

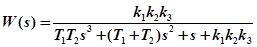Собственный оператор:

.

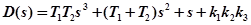Матрица Гурвица для рассматриваемого случая запишется следующим образом:

;

;

;

;

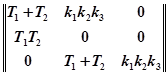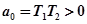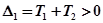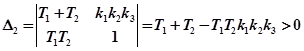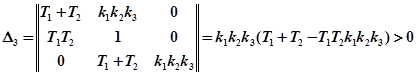
Последняя система структурно-устойчива, т.е. выбором коэффициентов T₁, T₂, k₁, k₂, k₃ можно добиться устойчивости. Из последнего выражения видно также, что увеличение запаса устойчивости реализуется за счет уменьшения коэффициентов усиления звеньев.

Пример: Система с неустойчивым инерционным звеном.

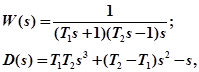
Матрица Гурвица для рассматриваемого случая запишется следующим образом:

;

;

;

.

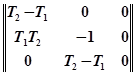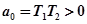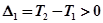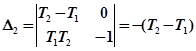Для того, чтобы система была устойчива, необходимо, чтобы 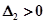, т. е. 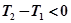. Это противоречит условию 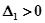. Таким образом, рассматриваемая система структурно неустойчива.