2015-05-13
1494
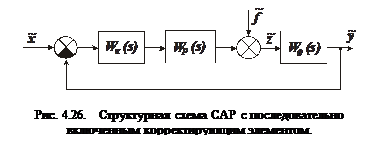
При последовательном соединении КУ передаточная функция САУ (рис. 4.26) в разомкнутом состоянии равна
,
 |
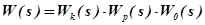где
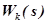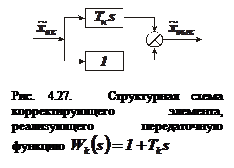
- передаточная функция КУ. Введение КУ в виде дифференцирующего звена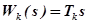 
увеличивает быстродействие регулятора, особенно на участках резкого отклонения регулируемого параметра. Таким образом, введение производной от регулируемого параметра компенсирует инерционное запаздывание в регуляторе и улучшает качество регулирования. Однако дифференцирующее КУ одновременно усиливает вредное действие высокочастотных помех, т. к. такое звено хорошо пропускает высокочастотные колебания по сравнению с низкочастотными и совсем не пропускает постоянную составляющую регулируемого параметра (отклонения регулируемого параметра). Поэтому нельзя вести регулирование только по производной от отклонения регулируемого параметра. Обычно дифференцирующее КУ включают параллельно величине рассогласования (рис. 4.27). В этом случае передаточная функция КУ равна
.
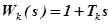Сигнал на выходе из КУ пропорционален как отклонению регулируемого параметра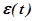 
, так и его производной 
.
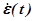Если написать выражение для модуля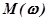 
и аргумента 
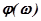частотной функции КУ
, 
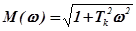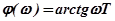
и разомкнутой системы
,
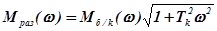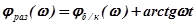, (4.13)
то можно сделать заключение, что введение КУ приводит к увеличению аргумента частотной функции разомкнутой САУ (вращает годограф Найквиста против часовой стрелки). Это приводит к увеличению запаса устойчивости системы регулирования. В выражениях (4.13) обозначено:
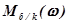- модуль передаточной функции разомкнутой системы до установки корректирующего устройства;
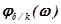- аргумент передаточной функции разомкнутой системы до установки КУ;
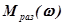- модуль передаточной функции системы после установки корректирующего устройства;
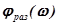- аргумент передаточной функции разомкнутой системы после установки КУ.
Последовательные КУ особенно целесообразно применять в электрических частях регуляторов, когда их можно набрать из электрических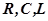 
- элементов.
Рассмотрим пример определения параметров КУ, включенного для коррекции характеристик чувствительного элемента температуры на входе в турбину двигателя. Известно, что термопара описывается уравнением апериодического звена и имеет передаточную функцию
,
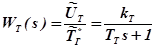где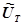 
- изображение по Лапласу напряжения на выходе из термопары;
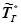- изображение по Лапласу температуры газа,
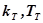- коэффициент передачи и постоянная времени термопары.
При ступенчатом изменении температуры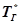 
напряжение на выходе из термопары 
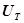изменяется по экспоненте (рис. 2.8). Время переходного процесса составляет 
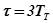. Для увеличения точности регулирования, особенно на переходных режимах работы двигателя необходимо уменьшать 
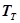. Термопары современных двигателей имеют постоянную времени 
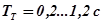, причем постоянная времени зависит не только от свойств материала спая, массы, но и от характера его обтекания, плотности газа. Уменьшение 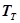за счет снижения размеров термопары приводит к снижению ее прочности и ресурса. Поэтому для улучшения динамических характеристик термопар применяют КУ в виде дифференцирующего 
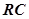-контура. Необходимо, чтобы на выходе из термопары сразу за изменением температуры 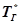следовало изменение напряжения 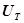. Это возможно, если термопара с КУ будет описываться уравнением пропорционального звена с коэффициентом 
.
.
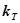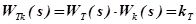Из последнего равенства получим выражение для требуемой передаточной функции КУ
.
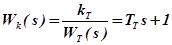Таким образом передаточная функция КУ имеет вид
.
 |
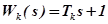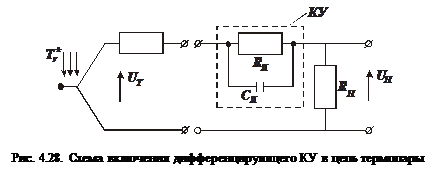Такую передаточную функцию можно реализовать электрической
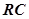-цепью (рис. 4.28). Тогда передаточная функция КУ определяется как отношение
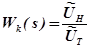, (4.14)
где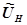 
- напряжение на входе в нагрузку, имеющую сопротивление 
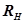. Для определения 
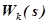в соответствие с равенством (4.14) воспользуемся законами Ома для замкнутой цепи
, 
,
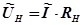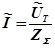где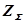 
- суммарный импеданс замкнутой цепи. Так как 
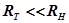и 
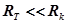, то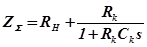 
. Тогда справедливо равенство
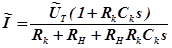
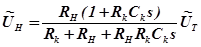
Обозначим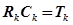 
, 
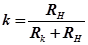, тогда выражение для 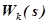примет вид
.
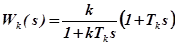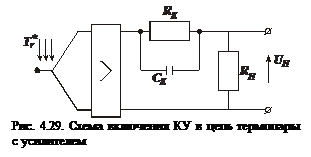Выражение 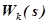реального КУ отличается от 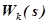идеального КУ сомножителем 
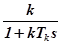. Чем меньше величина 
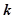, тем ближе выражение 
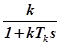к коэффициенту 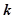, а следовательно и общее выражение 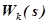к передаточной функции идеального КУ. Однако при этом сигнал на выходе из КУ ослабляется. Поэтому требуется подключить в цепь дополнительный усилитель (рис. 4.29). При этом коэффициент его усиления должен быть 
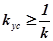. Ввиду того, что 
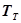зависит от режима работы двигателя, то ее величина будет переменна. В этом случае 
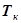делают также переменным в зависимости от режима работы двигателя. Однако такие системы требуют установки дополнительных чувствительных и исполнительных элементов, поэтому применяют обычно КУ с 
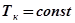, настроенного на наибольшее значение 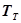в процессе работы двигателя.
 |
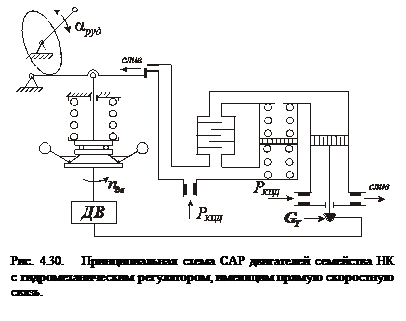Дифферецирующие КУ можно реализовать и в гидромеханических регуляторах, например, в агрегатах дозировки топлива (АДТ) двигателей семейства НК (рис. 4.30). Подпружиненный с обеих сторон поршень выполняет роль электрической емкости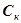 
, а дросселирующий элемент – сопротивления 
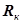. За входной параметр КУ можно принять перепад давления на нем, а за выходной – расход жидкости. Тогда уравнения КУ в малых приращениях примут вид
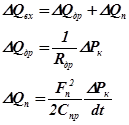(4.15)
где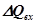 
- объемный расход жидкости на входе в КУ;
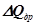- расход жидкости через дросселирующий элемент;
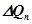- расход жидкости, обусловленный движением поршня;
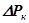- перепад давления на КУ;
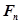- площадь торца поршня;
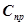- жесткость пружины КУ.
Переходя в (4.15) к изображениям по Лапласу, после преобразований получим:
,
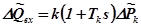где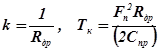 
- коэффициент передачи и постоянной времени КУ.
Из последнего выражения ясно, что чем больше сопротивление дросселя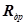 
, тем меньше коэффициент передачи КУ и больше постоянная времени 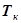. Во многих системах 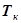изменяют в зависимости от внешних условий и режима работы двигателя за счет автоматического подключения дополнительных дроссельных пакетов различного гидравлического сопротивления.
В некоторых статических САУ с целью исключения статической ошибки регулирования последовательно в цепь регулятора включают интегрирующие КУ с передаточной функцией
.
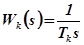Однако такая коррекция делает систему астатической, т. е. склонной к колебаниям в процессе регулирования. Поэтому чаще применяют регуляторы с местной изодромной обратной связью.
