Находят широкое применение при обработке относительно коротких дискретных последовательностей.
Рекурсивными фильтрами называются фильтры, в которых каждая выборка выходного сигнала формируется как взвешенная сумма некоторых предшествующих входных и выходных выборок.
Разностное уравнение такого фильтра 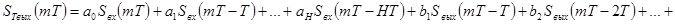
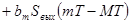 (1)
(1)
где 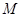 - количество отсчётов выходного сигнала в предшествующие моменты порядок рекурсивного фильтра.
- количество отсчётов выходного сигнала в предшествующие моменты порядок рекурсивного фильтра.
Структурная схема алгоритма фильтрации.
Принципиальное различие между трансверсальным и рекурсивным фильтрами заключается в свойствах их импульсных характеристик. В рекурсивном цифровом фильтре благодаря обратной связи число отсчётов теоретически бесконечно. БИХ – фильтрации.
Определим передаточную функцию рекурсивного цифрового фильтра.
Применим к разностному уравнению (1) преобразование Лапласа:
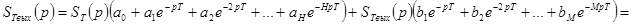
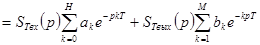 (2)
(2)
откуда следует, что 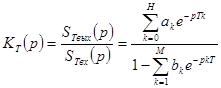 (3)
(3)
где 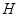 - число предшествующих входных отсчётов,
- число предшествующих входных отсчётов, 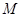 - число предшествующих выходных отсчётов.
- число предшествующих выходных отсчётов.
Полученную функцию можно трактовать как передаточную функцию каскадного соединения двух фильтров: одного с передаточной функцией 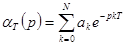 (4) и вторую с передаточной функцией
(4) и вторую с передаточной функцией 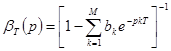 (5)
(5)
Таким образом 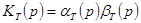 (6)
(6)
Такому представлению соответствует каноническая схема трансверсального фильтра.
Применим 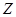 - преобразование к передаточной функции (3) получим
- преобразование к передаточной функции (3) получим 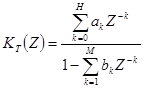 (7)
(7)
Фильтр осуществим при 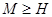 . Чтобы определить устойчив фильтр необходимо определить полюса функции (7). Фильтр устойчив если полюса функции расположены в плоскости единичного круга на плоскости
. Чтобы определить устойчив фильтр необходимо определить полюса функции (7). Фильтр устойчив если полюса функции расположены в плоскости единичного круга на плоскости 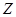 .
.
 2015-05-13
2015-05-13 1178
1178
