Определение. Если 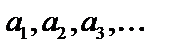 последовательность чисел, то выражение вида
последовательность чисел, то выражение вида 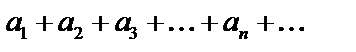 называют числовым рядом.
называют числовым рядом.
Записывают: 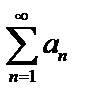 ,
, 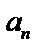 – называют общим членом ряда, а сумму первых «n» членов ряда
– называют общим членом ряда, а сумму первых «n» членов ряда 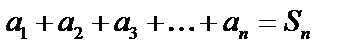 называют n -й частичной суммой ряда.
называют n -й частичной суммой ряда.
Определение. Если существует конечный предел 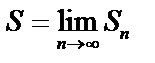 , то ряд называют сходящимся, а число S называют суммой ряда и записывают
, то ряд называют сходящимся, а число S называют суммой ряда и записывают
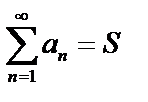
В противном случае ряд называют расходящимся.
Теорема (необходимый признак сходимости ряда). Если ряд 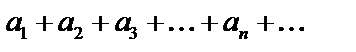 сходится, то его общий член
сходится, то его общий член 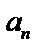 стремится к нулю при неограниченном возрастании номера n, т.е.
стремится к нулю при неограниченном возрастании номера n, т.е. 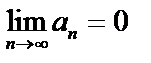 .
.
Следствие (достаточный признак расходимости ряда). Если общий член ряда не стремится к нулю при неограниченном возрастании его номера n, то ряд расходится.
Пример. Ряд 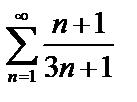 – расходится, т.к. его общий член
– расходится, т.к. его общий член 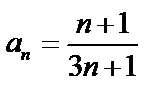 не стремится к нулю при
не стремится к нулю при 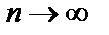 :
: 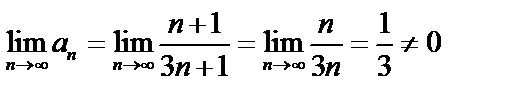 .
.
Замечание. Условие 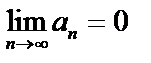 является необходимым для сходимости ряда, но не достаточным.
является необходимым для сходимости ряда, но не достаточным.
Пример. Гармонический ряд 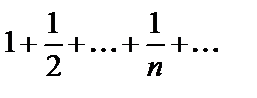 расходится, хотя
расходится, хотя 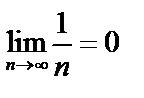 .
.
Определение. Знакоположительным рядом называется ряд, у которого все члены положительны, т.е. ряд 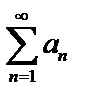 , где
, где 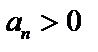 для всех
для всех 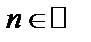 .
.
Рассмотрим некоторые наиболее часто встречающиеся признаки сходимости и расходимости рядов.
1. Первый признак сравнения.
Даны два ряда 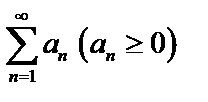 и
и 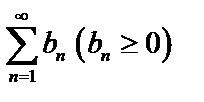 и начиная с некоторого номера
и начиная с некоторого номера 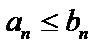 , тогда
, тогда
1) если 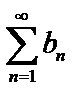 сходится, то и
сходится, то и 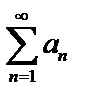 тоже сходится;
тоже сходится;
2) если 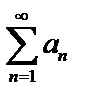 расходится, то и
расходится, то и 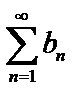 тоже расходится.
тоже расходится.
2. Второй признак сравнения (признак эквивалентности).
Даны два ряда 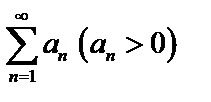 и
и 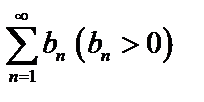 . Если
. Если 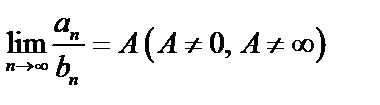 , то оба ряда ведут себя одинаково, т.е. одновременно сходятся или расходятся.
, то оба ряда ведут себя одинаково, т.е. одновременно сходятся или расходятся.
Замечание. Часто для сравнения используют
а) обобщенный гармонический ряд 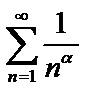 , который при
, который при 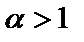 сходится, при
сходится, при 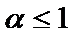 расходится;
расходится;
б) геометрический ряд 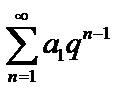 , который расходится при
, который расходится при 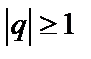 , а при
, а при 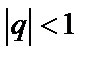 сходится к
сходится к 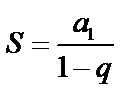 ,
,
т.е. 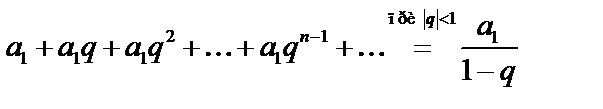
 2015-05-13
2015-05-13 2273
2273








