Пусть функции 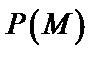 ,
, 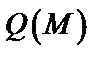 ,
, 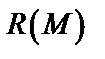 непрерывны в точках гладкой кривой
непрерывны в точках гладкой кривой 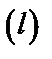 . Интегральной суммой для этих функций по координатам называется сумма вида
. Интегральной суммой для этих функций по координатам называется сумма вида
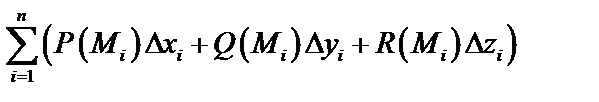 ,
,
где 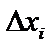 ,
, 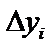 ,
, 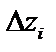 – проекции
– проекции 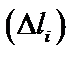 на оси
на оси 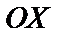 ,
, 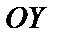 ,
, 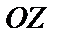 соответственно,
соответственно, 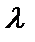 – шаг разбиения кривой
– шаг разбиения кривой 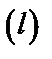 .
.
Криволинейным интегралом по координатам называется предел интегральной суммы при условии, что 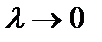 .
.
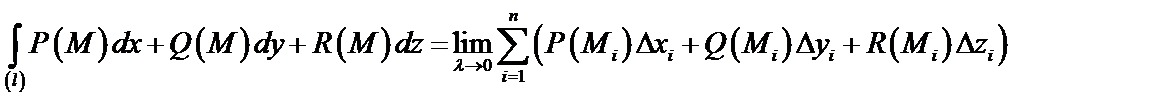 Если
Если 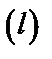 – кривая на плоскости, то криволинейный интеграл II рода имеет вид:
– кривая на плоскости, то криволинейный интеграл II рода имеет вид: 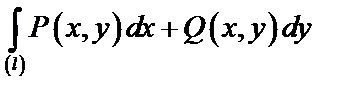 , причем
, причем 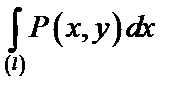 – криволинейный интеграл по координате «x»;
– криволинейный интеграл по координате «x»;
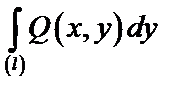 – криволинейный интеграл по координате «y».
– криволинейный интеграл по координате «y».
Пусть 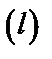 – гладкая ориентированная кривая на плоскости.
– гладкая ориентированная кривая на плоскости.
а) 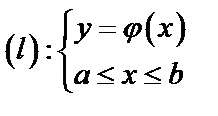
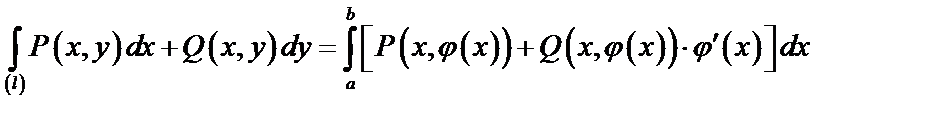
б) 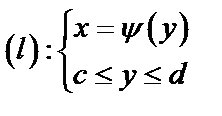
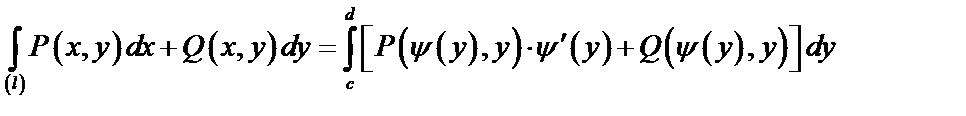
Вычисление криволинейного интеграла II рода можно заменить вычислением двух определенных интегралов: один интегралом по переменной «x», а второй по переменной «y».
в) 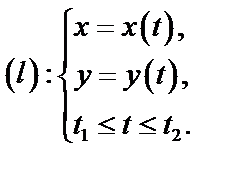
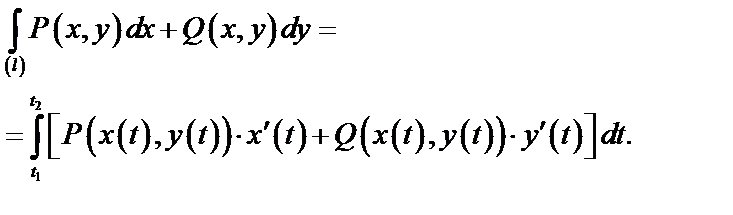 (49)
(49)
г) Пусть 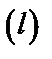 – гладкая ориентированная пространственная кривая т.е
– гладкая ориентированная пространственная кривая т.е
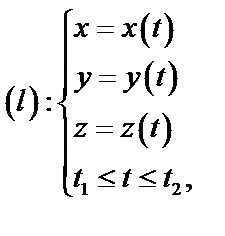 ,
,
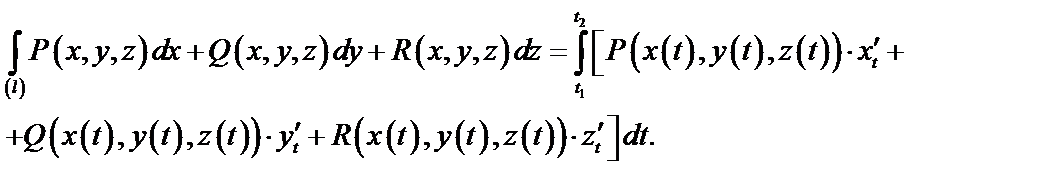
Замечание. При изменении направления пути интегрирования криволинейный интеграл II рода меняет свой знак на противоположный.
Криволинейный интеграл II рода есть работа, совершаемая переменной силой 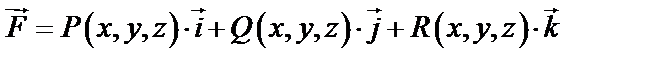 на криволинейном пути
на криволинейном пути 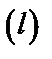 :
: 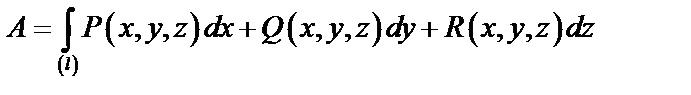 .
.
 2015-05-13
2015-05-13 479
479







