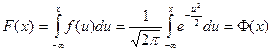Функция Лапласа и ее свойства. Вероятность попадания гауссовской СВ в заданный интервал. Правило трех сигма

- функция Лапласа. Она обладает следующими свойствами:

1) Ф(0)=1/2

2) Ф(-х)=1-Ф(х)

Иногда вместо функции Лапласа Ф(х) используют функцию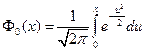

Она в свою очередь обладает следующими свойствами:

1) Ф₀(0)=0

2) Ф₀(-х)=-Ф₀(х)

3) Ф(х)=1/2+Ф₀(х), х>0

ФР СВ, имеющей нормальный ЗР также выражается через функцию

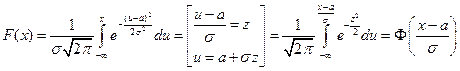
Вероятность попадания СВ Х, имеющей нормальный ЗР, на интервал [x₁, x₂) определяется по формуле: 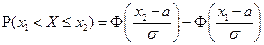. Наиболее просто вычисляются вероятности попадания нормальной СВ 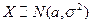на интервал длины 2 l c серединой в точке а.

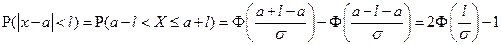
Полагая в последней формуле 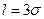и учитывая, что Ф(3)=0,9987, получаем: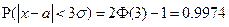

Полученный факт носит название «правила трех сигма». Оно означает, что практически все значения НСВ 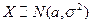принадлежат промежутку 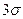(a - , a + 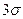) в том смысле, что вероятность того, что СВ 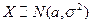примет значение, не принадлежащее данному промежутку пренебрежимо мала.