Производную показательной функции 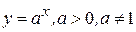 также можно найти с помощью метода логарифмического дифференцирования.
также можно найти с помощью метода логарифмического дифференцирования.
Для этого, прологарифмируем функцию по основанию 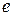 , получим:
, получим:
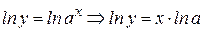 .
.
Продифференцируем обе части последнего равенства по аргументу 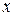 , учитывая, что
, учитывая, что 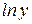 – сложная функция, так как y зависит от
– сложная функция, так как y зависит от 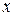
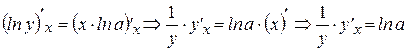 .
.
Откуда выразим 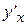 , учитывая, что
, учитывая, что 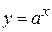 ;
; 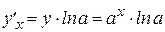 , то есть
, то есть
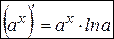 . (4)
. (4)
Теперь найдем производную функции 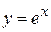 с помощью формулы (4)
с помощью формулы (4)
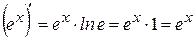 ,
,
то есть
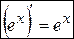 . (5)
. (5)
В результате применения правила дифференцирования сложной функции получим формулы для нахождения производных сложных функций 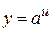 и
и 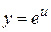 , где
, где 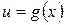
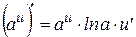 , (4’)
, (4’)
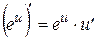 . (5’)
. (5’)
Примеры: Найти производные следующих функций:
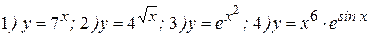
Решение:
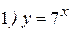
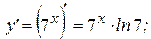
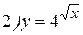
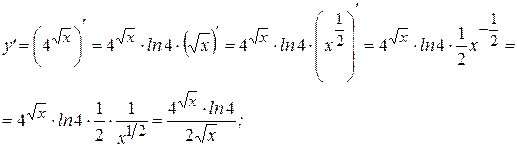
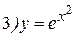
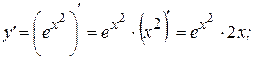
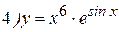
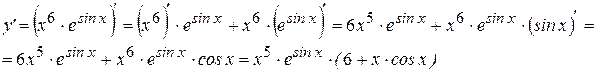
 2015-05-30
2015-05-30 926
926








