Найдем производную функции 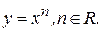
Для этого применим способ, который называется логарифмическим дифференцированием. Он заключается в том, что функцию вначале логарифмируют, а затем находят производную.
Итак, прологарифмируем функцию 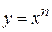 по основанию e:
по основанию e: 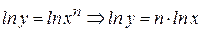 . Теперь продифференцируем обе части последнего равенства по аргументу
. Теперь продифференцируем обе части последнего равенства по аргументу 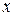 , учитывая, что
, учитывая, что 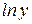 это сложная функция, так как
это сложная функция, так как 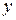 зависит от
зависит от 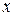
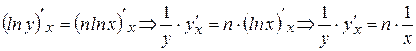 .
.
А теперь из этого равенства выразим искомую величину 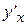 , учитывая, что
, учитывая, что 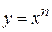 , получим
, получим
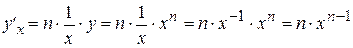 ,
,
то есть
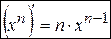 , где
, где 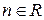 . (3)
. (3)
Воспользовавшись правилом дифференцирования сложной функции, найдем производную сложной функции
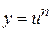 , где
, где 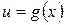 , получим
, получим 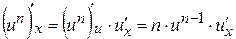 , то есть
, то есть
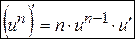 . (3’)
. (3’)
Примеры: Найти производные следующих функций:
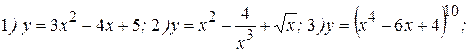
Решение:
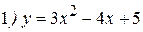
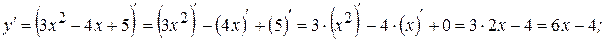
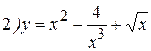
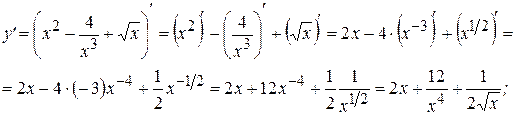
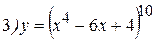
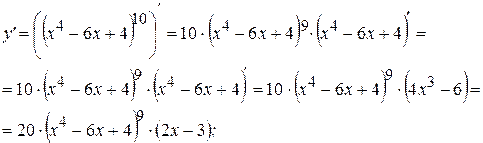
Замечание: Здесь можно выделить функцию 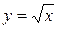 . Найдем ее производную с помощью формулы (2):
. Найдем ее производную с помощью формулы (2):
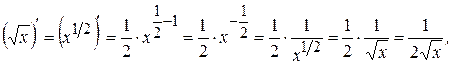 то есть
то есть
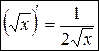 .
.
Для сложной функции 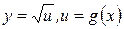 получим формулу при помощи правила
получим формулу при помощи правила
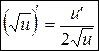 .
.
 2015-05-30
2015-05-30 1185
1185
