I Для перехода от неравномерных процессов к равномерным, истинное изменение какой-либо величины заменяют ее дифференциалом. Эта замена основана на том, что на протяжении малого промежутка времени всякий процесс приближается к равномерному.
Дадим общее определение дифференциала. Пусть дана функция 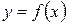 , дифференцируемая в точке x.Это означает, что функция в точке x имеет производную, то есть существует предел
, дифференцируемая в точке x.Это означает, что функция в точке x имеет производную, то есть существует предел 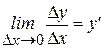 , следовательно для функции
, следовательно для функции 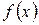 выполняется равенство
выполняется равенство
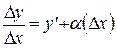 ,
,
где 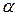 – бесконечно малая величина, то есть
– бесконечно малая величина, то есть 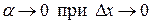 .
.
Умножив обе части этого равенства на 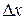 , получим
, получим
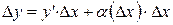 . (1)
. (1)
Здесь 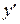 есть функция от
есть функция от 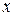 и не зависит от
и не зависит от 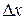 . Следовательно,
. Следовательно, 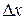 входит в первое слагаемое в первой степени (то есть линейно). Поэтому первое слагаемое представляет собой линейную часть приращения функции
входит в первое слагаемое в первой степени (то есть линейно). Поэтому первое слагаемое представляет собой линейную часть приращения функции 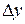 (про второе слагаемое этого сказать нельзя, так как
(про второе слагаемое этого сказать нельзя, так как 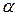 зависит от
зависит от 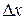 ).
).
Тогда при 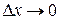 вторым слагаемым
вторым слагаемым 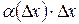 можно пренебречь, и первое слагаемое
можно пренебречь, и первое слагаемое 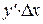 будет являться главной частью приращения функции (исключая случай, когда
будет являться главной частью приращения функции (исключая случай, когда 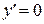 ).
).
Главная часть приращения функции, линейная относительно приращения независимой переменной, называется дифференциалом функции и обозначается знаком 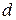 , то есть
, то есть
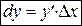 . (2)
. (2)
Для функции 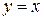 получаем
получаем 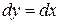 , так как
, так как 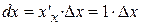 , откуда
, откуда
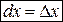 . (3)
. (3)
Следовательно, дифференциал независимой переменной равен приращению этой переменной.
Из формул (2) и (3) следует, что
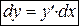 . (4)
. (4)
То есть дифференциал функции равен произведению ее производной на дифференциал независимой переменной.
Пример: Найти дифференциалы следующих функций:
1) 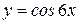 ; 2)
; 2) 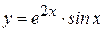 ; 3)
; 3) 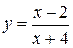 ;
;
Решение:
1)Воспользуемся формулой (4) и найдем производную функции 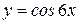 :
:
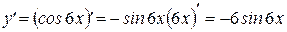 . Таким образом,
. Таким образом, 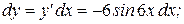
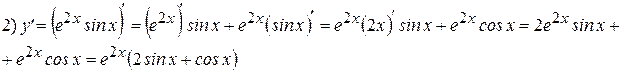 Откуда,
Откуда, 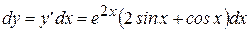 ;
;
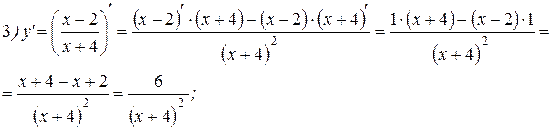
Откуда, 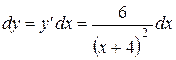
Пример: Найти дифференциал функции 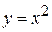 в точке
в точке 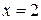 при
при 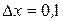 .
.
Решение:
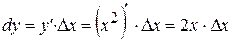 . Подставив в найденное выражение
. Подставив в найденное выражение 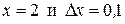 найдем нужное нам значение:
найдем нужное нам значение:
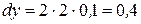
 2015-05-30
2015-05-30 1572
1572
