I Геометрический смысл дифференциала

Рассмотрим график непрерывной функции .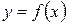

Рис. 9

Производная функции в точке с абсциссой 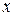равна тангенсу угла наклона касательной к положительному направлению оси 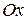, то есть

.

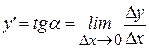Из рисунка видно, что касательная разбивает приращение функции 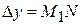на два отрезка: 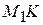, соответствующий в равенстве (1) слагаемому 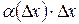, и 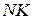, соответствующий в равенстве (1) слагаемому .

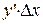Если 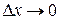(точка 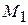стремится занять положение 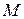), то отрезок 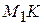уменьшается значительно быстрее, чем отрезок .

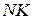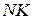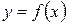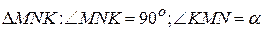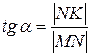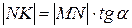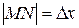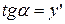Таким образом, приращение ординаты касательной является главной частью приращения функции . Из : находим , откуда . Далее: , а , то .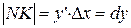

Итак, сформулируем геометрический смысл дифференциала:

Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение .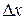

ЛИТЕРАТУРА

1 Валуцэ И.И., Дилигул Г.Д. Математика для техникумов. – М.: Наука, 1980. – Гл. 5. – ÍÍ1-13.

2 Доброхотова М.А., Сафронов А.Н. Функция, ее предел и производная. – М.: Издательство «Просвещение», 1969. – Гл. 6. – ÍÍ51-61, Í65. – Гл. 7. – ÍÍ67-75.

3 Зайцев И.А. Элементы высшей математики. – М.: Наука, 1974.

4 Лисичкин В.Т., Соловейчик И.Л. Математика. Учебное пособие для техникумов. – М.: Высшая школа, 1991. – Гл. 4. – ÍÍ3-7.

5 Яковлев Г.Н. Алгебра и начала анализа, часть I. – М.: Наука, 1987. – Гл. 6, Гл. 7. – ÍÍ34-39.