Сформулировать теорему о связи интеграла Римана и интеграла Лебега для ограниченной функции, заданной на отрезке

Теорема:

Если для функции, заданной на отрезке [a,b], существует собственный интеграл Римана 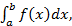то она суммируема и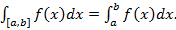

9. Определение и примеры векторных пространств над полем R, в том числе бесконечномерных.

Определение: (пусть K поле действительных или комплексных чисел (поле скаляров)).

Непустое множество E называется векторным (линейным) пространством над полем K, если для любых двух его элементов x и y определена их сумма x+y элемент того же множества и для любого 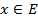и любого 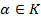определено произведение αx, являющееся элементом множества E, причем эти операции удовлетворяют следующим условиям:

1. x+y=y+x;

2. (x+y)+z=x+(y+z);

3. В E существует элемент θ такой, что для любого 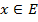справедливо x+θ=x;

4. Для каждого 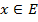существует элемент 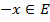, что выполняется x+(-x)=θ;

5. ;

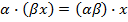6. ;

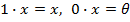7. ;

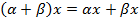8. ;

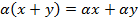Пример:

* Множество всевозможных векторов (в трехмерном пространстве, на плоскости или прямой) образуют векторное пространство.

* Непрерывные функции, заданные на некотором отрезке [a,b], с обычными операциями сложения функций и умножения их на число образуют векторное пространство C[a,b], являющееся одним из важнейших для анализа.