Пусть 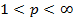 и
и 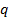 – число, сопряжённое к нему (
– число, сопряжённое к нему (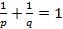 ). Тогда для любых функций
). Тогда для любых функций 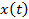 и
и 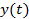 , заданных на
, заданных на  , для которых существуют интегралы
, для которых существуют интегралы
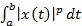 и
и 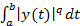
имеет место неравенство Гельдера
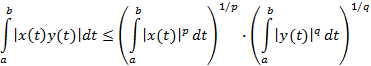
Пусть 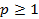 и пусть функции x(t) и y(t) таковы, что существуют и конечны интегралы
и пусть функции x(t) и y(t) таковы, что существуют и конечны интегралы 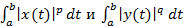 , тогда справедливо неравенство Минковского
, тогда справедливо неравенство Минковского
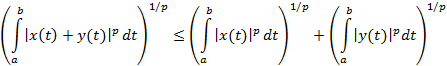
17. Определение пространства Lp[a,b].
Пространством 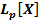 называется нормированное векторное пространство, элементами которого являются классы эквивалентных между собой интегрируемых по Лебегу функций со степенью p и нормой
называется нормированное векторное пространство, элементами которого являются классы эквивалентных между собой интегрируемых по Лебегу функций со степенью p и нормой
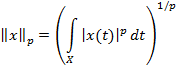
Сходимость в пространстве 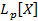 называется сходимостью в среднем со степенью p.
называется сходимостью в среднем со степенью p.
Определение и примеры открытых и замкнутых множеств в нормированных векторных пространствах.
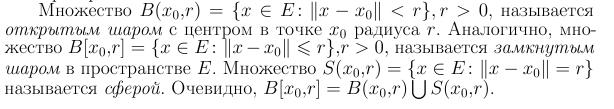

 2015-05-22
2015-05-22 849
849








