ГЛАВА 1. Нечеткие множества
В классической теории множеств принадлежность элемента x некоторому множеству A записывается в формализованном виде:
x Î A.
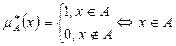 |
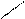 Эта формальная запись может также представляться с помощью характеристической функции:
Эта формальная запись может также представляться с помощью характеристической функции: Символ 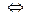 обозначает эквивалентность.
обозначает эквивалентность.
Принадлежность множества к некоторому одномерному множеству A можно представить в графической форме. Пусть имеем одномерное арифметическое пространство – R 1, в котором заданы два непересекающихся подмножества A и B: A Ì R 1, B Ì R 1, A Ç B =Æ.
Тогда принадлежность x подмножеству A можно представить в виде прямоугольника PA (рис. 1.1а), принадлежность подмножеству B в виде прямоугольника PB(рис. 1.1б). Обычно эти графические формы принадлежности совмещаются и в результате получается совокупность из 2-х прямоугольников (рис. 1.1в). Принадлежность некоторому двумерному подмножеству представляется параллелепипедом в 3-х мерном пространстве, а принадлежность n - мерному подмножеству соответственно (n+1) - мерным параллелепипедом.
В классической (четкой) теории множеств четкое подмножество A определяется как совокупность упорядоченных пар { x, mA * (x)}, где { ×} – символ совокупности. В одномерном случае x Î R 1 , в общем x Î Rn. Выбор арифметического пространства Rn обусловлен тем,что в теории управления с переменными x обычно связывают некоторые физические величины (температура, давление, расход и т.д.), которые получают с измерительных датчиков, установленных на объекте управления.
Факту принадлежности можно также придать лингвистическую форму. Пусть в R 1 задана некоторая физическая величина, например, температура воды, которая измеряется соответствующим датчиком. Будем ассоциировать с подмножеством A диапазон изменения температуры 0°С до 50°, а с подмножеством B ее изменение в диапазоне от 50С° до 100°С. В лингвистической интерпретации принадлежность измеренной температуры подмножеству A будет соответствовать лингвистической переменной “холодная вода”, а подмножеству B – “горячая вода”. Аналогичная интерпретация может быть дана и для других физических величин: давление –“низкое” (подмножество A) или “высокое” (подмножество B), линейная скорость перемещения “маленькая” (подмножество A) или “большая” (подмножество B) и т.д. Если использовать кодирование символами 0 и 1 для упомянутых выше лингвистических переменных, то получим соответствие: “холодная” - 0, “горячая ”-1, “маленькая” – 0, “большая” –1 и т.д. В этой интерпретации не представляется возможным отразить промежуточные состояния температуры воды типа: “прохладная” вода, «теплая» вода, т.к. переменная принадлежности тому или иному подмножеству принимает только два значения 0 или 1, что подразумевает наличие четкой или резкой границы между подмножествами.
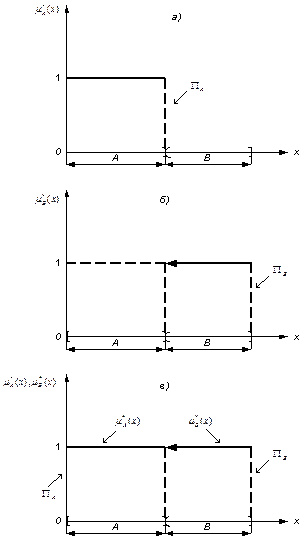
Рис.1.1 Графическое представление принадлежности в классической теории множеств.
В классической теории множеств принадлежность элемента одному подмножеству исключает одновременную принадлежность его другому множеству.
Таким образом, в математических терминах характеристическая функция mA*(x) осуществляет отображение некоторого дискретного или непрерывного подмножества A в множество R1, которое содержит всего лишь два элемента 0 и 1:

m A *(x):A ®R1={0,1}.
Из определения следует, что областью определения m A*(x)является дискретное или непрерывное подмножество, а область значений есть дискретное множество {0,1}. В дискретной математике для исчисления высказываний с функциями, имеющими двоичные значения, используется булева алгебра, которая является теоретической базой вычислительной техники.
Если область значений одномерного отображения mA (x)Î[0,1] Ì R 1, тогда mA (x) называется одномерной функцией принадлежности (membership function). Для исчисления высказываний с такими функциями, принимающими непрерывные значения на отрезке [0,1],используется нечеткая логика, которая является одним из разделов теории нечетких множеств. Сопоставление характеристической функции mA *(x)классической теории множеств с функцией принадлежности mA (x)теории нечетких множеств показывает, чтохарактеристическая функция является частным случаем функции принадлежности, т.к. бинарная совокупность{0,1}Ì[0,1]. Графическая трактовка одномерной функции принадлежности представлена на рис.1.2. Подмножество A Ì R 1 имеет функцию принадлежности mA (x) (рис.1.2а), подмножество B Ì R 1 функцию принадлежности mВ (x) (рис.1.2б), их совместное положение изображено на рис.1.2в.

Рис.1.2 Графическое представление принадлежности в теории нечетких множеств.
Из рис.1.2а следует, что элемент x 1 Î А имеет mA (x 1) = 1, а элемент x 2 Î А соответственно mA (x 2)=0.8, поэтому в теории нечетких множеств принято говорить, что элемент x 1принадлежит множеству А полностью, а элемент x 2принадлежит множеству А частично. Аналогично из рис.1.2б имеем x 4 Î В полностью (mВ (x 4) = 1), x 3Î В частично (mВ (x 3)=0.8). Соответственно из рис.1.2в имеем: x 2ÎА частично с весом 0.8 (mА (x 2)=0.8) и x 2Î В частично – с весом 0.2 (mВ (x 2)=0.2). Элемент x 3Î А частично с весом 0.2 (mА (x 3)=0.2) и x 3Î частично с весом 0.8 (mВ (x 3)=0.8).
Таким образом, граница между двумя множествами А и В является размытой или нечеткой и переход элементов из одного множества в другое происходит плавно, без скачков. В классической теории множеств этот переход осуществляется скачкообразно, и оба множества имеют четкую границу между собой. В таблице 1.1 представлено сопоставление характеристической функции mA *(x) теории четких множеств с функцией принадлежности mA (x) теории нечетких множеств.
Таблица 1.1. Сопоставление характеристической функции с функцией принадлежностей
| Теория четких множеств характеристическая функция mA *(x) | Теория нечетких множеств функция принадлежности mA (x) |
| m: А®{0,1} ÌR1 | m: А®[0,1] ÌR1 |
Наличие между нечеткими множествами размытых границ можно интерпретировать в лингвистической форме (рис. 1.3). Для температуры воды будем предполагать, что температура в 15°С и ее окрестности являются «холодной» водой, температура в 85°С и ее окрестности ассоциируются

Рис. 1.3 Количественное представление нечетких логических переменных «холодная», «горячая» вода.
с «горячей» водой (рис. 1.3а,б).
Тогда нечетким лингвистическим переменным «холодная», «горячая» можно дать количественную форму с использованием функций принадлежностей. Температура в 50°С частично с весом 0.5 является «холодной» и с весом 0.5 «горячей» (рис.1.3в). Отметим, что имеет место условие нормировки: mA (x)+ mВ (x)=1.
Одномерное нечеткое подмножество А Ì R 1 определяется как совокупность упорядоченных пар { x, mA (x)}, x Î R 1. В различных источниках используется эквивалентные способы представления нечетких множеств:
А ={ x ¤ mA (x)}Û А ={ mA (x)¤ x } Û А ={(x; mA (x))} Û
 |
А ={(m A (x); x)} Û Û 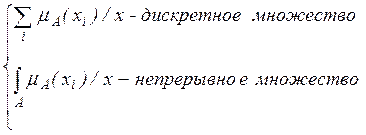
Здесь символы S и ò понимаются как объединение. Аналогичным способом представляются четкие множества с заменой mA (x) на mA *(x).
Пример. Пусть Е ={1,2,3,4,5} – четкое дискретное множество, А = {2,3,5}-четкое дискретное подмножество множества Е, т.е. А Ì Е. Тогда подмножество А может быть представлено в следующих эквивалентных формах:
А ={(1;0),(2;1),(3;1),(4;0),(5,1)} Û А ={1/0+2/1+3/1+4/0+5/1) Û
А ={ 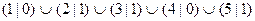 }.
}.

Графическое представление А изображено на рис.1.4. Четкое число xiÎR1в теории нечетких множеств определяется с помощью одиночной (singlton) функции принадлежности (рис.1.5)
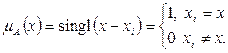
Пример. Е={1,2,3,4,5} –дискретное множество, ЕÉА –нечеткое дискретное подмножество с заданной функцией принадлежности (рис.1.6), тогда А может быть представлено в следующих эквивалентных формах А={(1;0),(2;0.51),(3;1),(4;0.5),(5,0)} Û А={1/0+2/0.5+3/1+4/0.5+5/0} Û
А={1/0 U 2/0.5 U 3/1 U 4/0.5 U 5/0}.
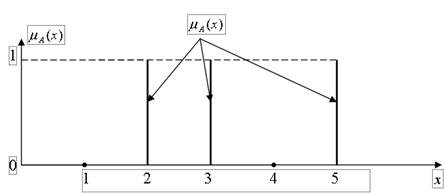
Рис. 1.4. Четкое дискретное подмножество А.
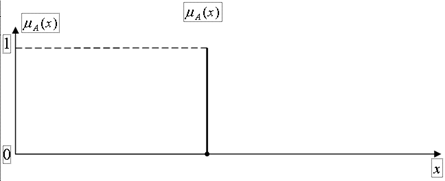
Рис. 1.5. Одиночная функция принадлежностей, представляющая четкое число 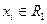 в теории нечетких множеств.
в теории нечетких множеств.
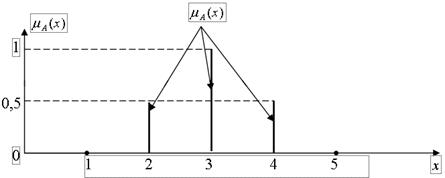
Рис. 1.6. Нечеткое дискретное подмножество А.
Пример. ЕÌR1 , ЕÉА –нечеткое непрерывное подмножество с функцией принадлежности
m A (x)=max(y1-½x-2½; y2=0), xÎ R1, (1.2)
тогда А может быть представлено в форме (рис.1.7):
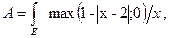 |
где, как и ранее, символ ò обозначает объединение. При использовании вычислительных устройств непрерывная функция принадлежности представляется в дискретной форме. После аппроксимации непрерывной функции принадлежности mA(x)треугольного типа ступенчатой функцией m A*(x) получим нечеткое дискретное подмножество А*, которое в первом приближении аппроксимирует непрерывное нечеткое подмножество А и может быть также записано в следующих эквивалентных формах (рис.1.8)
А»А * = {(1;0),(1.25;0.25),(1.5;0.5),(1.75;0.75),(2,1), (2.25;0.75),
(2.5;0.5),(2.75;0.25),(3,0)}º1/0+1.25/0.25+1.5/0.5+1.75/0.75+2/1+
+2.25/0.75+2.5/0.5+2.75/0.25+3/0º
1/0 U 1.25/0.25 U 1.5/0.5 U 1.75/0.75 U 2/1 U 2.25/0.75 U2.5/0.
5U 2.75/0.25 U 3/0.
Помимо приведенных выше функций принадлежности треугольного типа и одиночной в теории нечеткого управления широко используются функции трапецеидальной и колоколообразной формы (рис.1.9):
m A (x)=min{max(a-k½x-b½;0);1} - трапецеидальная, a,b – заданные числа, k- показатель нечеткости; xÎ R1;
m A (x)=exp{-(x-m)2/d2} - колоколообразная (нормальная); m- заданное число, d-показатель нечеткости, xÎ R1.
При решении научно-исследовательских задач нечеткого управления также могут быть использованы следующие функции принадлежности:
m A (x)=exp(-kx), x>0, m A (x)=1-axk, 0£x£ a-1/k; m A (x)=(1+kx2)-1, k>1.
Обзор простейших функций принадлежности, которые ассоциируютсяс нечеткими утверждениями «величина х – мала», «величина | х | – мала», «величина х – велика», «величина | х | – велика» приведен в [6].
Нечеткое множество с одномерной функцией принадлежности m A(x)принято называть нечетким множеством 1-го рода.
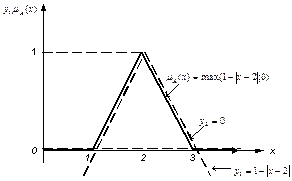
|
|
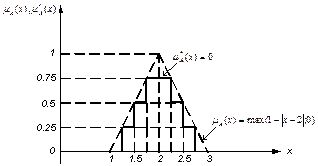
|

|
Различают также нечеткие множества 2-го рода; в этом случае функция принадлежности 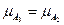 (
(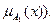

Для нечеткого множества n-го рода, соответственно, 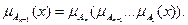
В современных разделах теории нечетких множеств активно изучается теория вероятностей нечетких множеств (глава 5), для которых
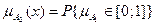 , где Р{×} – вероятность того, что случайная величина
, где Р{×} – вероятность того, что случайная величина 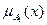 принимает значения из промежутка[0;1].
принимает значения из промежутка[0;1].
Изучаются другие типы нечетких множеств с определением функций принадлежностей на булевых переменных, решетках, сетях и т.д. Обобщаются традиционные разделы математики в нечеткой постановке: нечеткая статистическая проверка гипотез, нечеткий регрессионный анализ, нечеткие марковские случайные процессы, нечеткие дифференциальные уравнения и другие разделы.
Двумерное нечеткое множество А с использованием двумерной функции принадлежности mA (x 1, x 2) определяется как совокупность:
А = { A 1´ A 2; mA (x 1, x 2)},
где A 1´ A 2-прямое (декартово) произведение; x1, x2 Î R1. На рис.1.10 представлено нечеткое множество А с двумерной функцией принадлежности пирамидального типа:
mA (x 1, x 2)= max{ а - k 1ê x 1- b ê- k 2ê x 2-c ê; (x 1=0, x 2=0)},
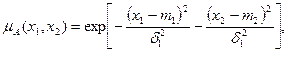 |
где a, b, c - заданные числа, k 1, k 2 – показатели нечеткости, а на рис.1.11 с двумерной колоколообразной функцией:
где m1, m2 - заданные числа, d 1, d 2 – показатели нечеткости.
Многомерное нечеткое множество А определяется как совокупность:
А = { A 1´ …´ A n; mA (x 1 ,…, x 2) }.
Многомерная пирамидальная функция принадлежности:
mA (x 1,.., xn)= max{ а - k 1ê x 1 - b 1ê- …. kn ê xn - bn ê; (x 1=0,…, xn =0) },
где 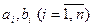 – заданные числа; ki - показатели нечеткости.
– заданные числа; ki - показатели нечеткости.
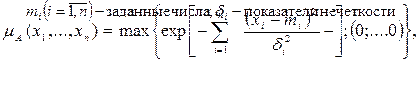 |
Многомерная колоколообразная функция принадлежности:
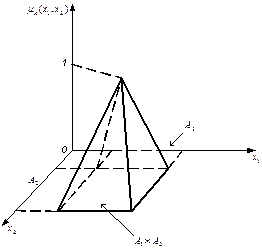
|
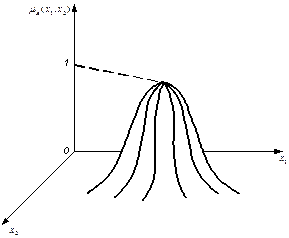
|
Нечеткое множество с многомерной функцией принадлежности помимо названия «многомерное нечеткое множество» имеет эквивалентное название «нечеткое отношение» (fuzzy relation).
По аналогии с (1.1) оно записывается в виде:
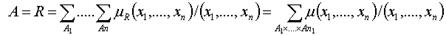
- многомерное нечеткое дискретное множество.
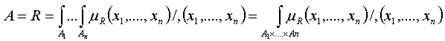
- многомерное нечеткое непрерывное множество.
Здесь символ R – аббревиатура Relation –отношение.
Например, двумерное нечеткое дискретное множество А с mA(x1,x2)=max(1-½x1-x2½/2;(0;0))на дискретной области x 1, x 2:0;1;2;….,10имеет представление A = R = = 0/(0;0)+0/(0;1)+…..+1/2/(0;9)+1/(0;10)+….+1/(10;0)+1/2/(10;1)+ +0/(10;2)+…+0/(10;10) или в матричной форме:
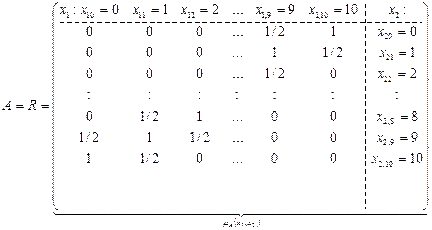
1.2. Свойства нечетких множеств.
При анализе работы нечеткого регулятора важную роль играют свойства нечетких множеств, перечислим некоторые из них (рис.1.12-1.17).
Высота (height-hgt) нечеткого множества А:
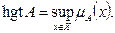
Нечеткое множество А с hgt А =1 называется нормальным, а при hgt А <1 субнормальным.
Ядро (core, kernal, nucleus) или центр нечеткого множества А:
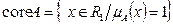
Основание (support-supp) нечеткого множества А:
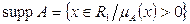
Если supp А < ¥, то основание называется компактным основанием, т.е. совокупность точек является ограниченной и замкнутой. При supp А = ± ¥ основание называется некомпактным.
Поперечными точками (crossover points) нечеткого множества А называется совокупность:
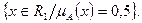
Уровень a нечеткого множества А или a -разрез (сечение) нечеткого множества А:
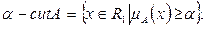
 2015-05-22
2015-05-22 2454
2454